初中数学相似多边形的性质试题

如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）

A．∠ABP=∠C	B．∠APB=∠ABC
C．	D．

如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（ ）

A．4

B．7

C．3

D．12

已知，△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，当BC=1，对应边EF的长是（ ）

A．

B．2

C．3

D．4

已知ABC∽A₁B₁C₁，AB:A₁B₁=2:3，若S_ABC=12，则=    ．

如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是     米．

如图所示的两个四边形相似，则的度数是     ．

下列四个三角形中，与左图的三角形相似的是 （      ）

已知△ABC∽△DEF，与的相似比为4:1，则与对应边上的高之比为            ．

在△ABC中，D．E为边AB、AC的中点，已知△ADE的面积为4，那么△ABC的面积是（ ）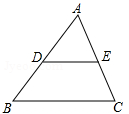

A．8      B．12      C．16      D．20

如图，AD∥BE∥CF，直线l₁，l₂与这三条平行线分别交于点A，B，C和点D，E，F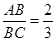，，DE=6，则EF=     ．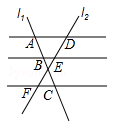

若△ADE∽△ACB，且，DE=10，则BC=       ．

如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD．若B（1，0），则点C的坐标为（ ）

A．（1，2）      B．（1，1）      C．（，）      D．（2，1）

如图，A，B两地被一座小山阻隔，为测量A，B两地之间的距离，在地面上选一点C，连接CA，CB，分别取CA，CB的中点D、E，测得DE的长度为360米，则A、B两地之间的距离是         米．

如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（    ）

A．AB=24m             B．MN∥AB      C．△CMN∽△CAB      D．CM：MA=1：2

如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是边AD，AB的中点，EF交AC于点H，则的值为（  ）

A．

B．1

C．

D．