(本题满分7分.)如图7,反比例函数 的图像与一次函数
的图像与一次函数 的图象交于点A、B,其中A(1,2).
的图象交于点A、B,其中A(1,2).
(1)求m,b的值;
(2)求点B的坐标,并写出 时,
时, 的取值范
的取值范 围.
围.
(11·钦州)
如图,在平面直角坐标系中,点O为原点,反比例函数y= 的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
(11·柳州)
如图,直线y=kx+k(k≠0)与双曲线 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.
(1)求m的取值范围和点A的坐标; (2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
如图,已知直线AB与x轴交于点C,与双曲线 交于A(3,
交于A(3, )、B(﹣5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
)、B(﹣5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).
(1)求点D的坐标;
(2)求经过点C的反比例函数解析式.
(本题6分) (湖南湘西,22,6分)如图,已知反比例函数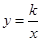 的图象经过点A(1,2).
的图象经过点A(1,2).
(1)求k的值.
(2)过点A分别作x轴和y轴的垂线,垂足为B和C,求矩形ABOC的面积.
如图,已知反比例函数 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).
⑴求直线y=ax+b的解析式;
⑵设直线 y=ax+b与x轴交于点M,求AM的长.
y=ax+b与x轴交于点M,求AM的长.
如图,已知A,B两点的坐标分别为A(0, ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转 α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
右图中曲线是反比例函数 的图象的一支.
的图象的一支.
(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)若一次函数 的图象与反比例函数的图象交于点A,与x轴交于点B,△
的图象与反比例函数的图象交于点A,与x轴交于点B,△
AOB的面积为2,求n的值.
如图,正比例函数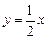 的图象与反比例函数
的图象与反比例函数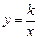
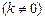 在第一象限
在第一象限
的图象交于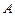 点,过
点,过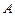 点作
点作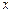 轴的垂线,垂足为
轴的垂线,垂足为 ,已知
,已知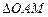 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果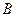 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点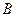 与点
与点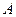 不重合),且
不重合),且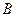 点的横坐标为1,在
点的横坐标为1,在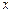 轴上求一点
轴上求一点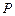 ,使
,使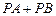 最小.
最小.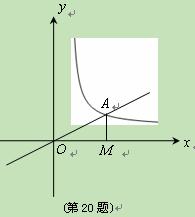
在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是BC上的一个动点(不与B、C重合),过F点的反比例函数 的图象与AC边交于点E.
的图象与AC边交于点E.
(1)求证:AE•AO=BF•BO;
(2)若点E的坐标为(2,4),求经过O、E、F三点的抛物线的解析式;
(3)是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出此时的OF的长:若不存在,请说明理由.
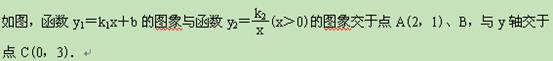
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时y1与y2的大小.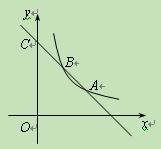
如图所示,直线 的方程为
的方程为 ,直线
,直线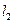 的方程为
的方程为 ,且两直线相交于点P,过点P的双曲线
,且两直线相交于点P,过点P的双曲线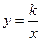 与直线
与直线 的另一交点为Q(3,m).
的另一交点为Q(3,m).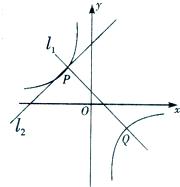
(1)求双曲线的解析式.
(2)根据图象直接写出不等式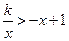 的解集.
的解集.