初中数学平行线分线段成比例解答题

如图，在平面直角坐标系中，函数的图象与一次函数的图象的交点为．

（1）求一次函数的解析式；
（2）设一次函数的图象与轴交于点，若是轴上一点，且满足的面积是4，求点的坐标．

如图，反比例函数y=（k＞0）与矩形OABC在第一象限相交于D、E两点，OA=2，OC=4，连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .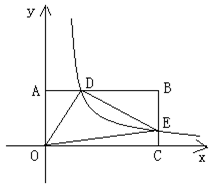

（1）①点B的坐标为；②SS（填“＞”、“＜”、“=”）；
（2）当点D为线段AB的中点时，求k的值及点E的坐标；
（3）当S+S=2时，试判断△ODE的形状，并求△ODE的面积.

反比例函数的图象与一次函数y=ax+b的图象交于A（1，3）和B（n,-1）两点.

（1）求这两个函数的解析式，并画出草图;
（2）根据图象回答当x取何值时，反比例函数的值大于一次函数的值;
（3）连接OA、OB, 求⊿AOB的面积.

你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度是面条的粗细（横截面积）的反比例函数，其图像如图所示.


（1）写出与的函数关系式；
（2）若面条的总长度是50m时，面条的粗细是多少？
（3）当面条的粗细应不小于，面条的总长度最长是多少？

如图，直线y ＝kx(k＞0)与双曲线交于A（x₁，y₁），B（x₂，y₂）两点，则2x₁y₂－7x₂y₁＝__

一定质量的氧气，它的密度是它的体积的反比例函数．当时，．
（1）求与V的函关系式；
（2）求当时氧气的密度．

已知与－2成反比例，且当=4时，=5， 求：
（1）与之间的函数关系式；
（2）当时，求的值．

某商场出售一批进价为2元的贺卡，在市场营销中发现商品的日销售单价x元与日销售量y个之间有如下关系：

x（元/个）	3	4	5	6
y（个）	20	15	12	10

（1）根据表中数据，在直角坐标系描出实数对（x，y）的对应点
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为W元，试求出W与x之间的函数关系式，若物价局规定此贺卡的售价最高不能超过10元/个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？

已知反比例函数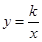的图象经过点.
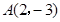（1）求的值；
（2）当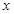取什么值时，函数的值大于0？

已知一个反比例函数的图象经过点．
（Ⅰ）求这个函数的解析式；
（Ⅱ）判断点是否在这个函数的图象上；
（Ⅲ）当时，求自变量的值．

如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在轴的正半轴上，点A在反比例函数（＞0）的图象上，点D的坐标为（4，3）.

（1）求的值；
（2）若菱形ABCD向右平移，使点D落在反比例函数（＞0）的图象上，求菱形ABCD平移的距离.

已知：点（1,3）在函数的图象上，矩形ABCD的边BC在轴上，E是对角线BD的中点，函数的图象又经过A，E两点，点E的横坐标为m，解答下列问题：

（1）求k的值；
（2）求点C的横坐标（用m表示）
（3）当∠ABD=45º时，求m的值.

在平面直角坐标系xOy中，一次函数y=kx+b与反比例函数y=的图象交于A(1,6)，B(a,3)两点.

（1）求k，k的值；
（2）如图，点D在x轴上，在梯形OBCD中，BC∥OD,OB=DC,过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为18时，求PE：PC的值.

如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=．
（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．

两个反比例函数和在第一象限内的图象如图所示，点P在的图象上，PC⊥x轴于点C，交的图象于点A，PD⊥y轴于点D，交的图象于点B，当点P在的图象上运动时，以下结论：
①△ODB与△OCA的面积相等；
②四边形PAOB的面积不会发生变化；
③PA与PB始终相等；
④当点A是PC的中点时，点B一定是PD的中点．
其中一定正确的结论有哪几个？对正确的结论要说明理由！