初中数学平行线分线段成比例解答题

在Rt△ABC中，∠C=90°，∠A=30°，BC=2．若将此直角三角形的一条直角边BC或AC与x轴重合，使点A或点B刚好在反比例函数 （x＞0）的图象上时，设△ABC在第一象限部分的面积分别记做S₁、S₂（如图1、图2所示）D是斜边与y轴的交点，通过计算比较S₁、S₂的大小．

如图，的图象与反比例函数的图象相交于点A（2，3）和点B，与x轴相交于点C（8，0）．

（1）求这两个函数的表达式；
（2）请直接写出当x取何值时，y₁＞y₂．

如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.

（1）求反比例函数的解析式；
（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.

如图，已知点A（a，3）是一次函数y₁=x+b图象与反比例函数y₂=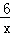图象的一个交点．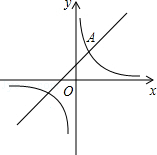

（1）求一次函数的解析式；
（2）在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围．

如图，某一次函数与反比例函数的图象相交于A（－2，－5）、B（5，n）两点．

(1) 求这两个函数的解析式；
(2) 联结OA，OB．求△AOB的面积．

已知图中的曲线是函数 (m为常数)图象的一支.

（1）求常数m的取值范围；
（2）若该函数的图象与正比例函数图象在第一象限的交点为A（2，n），求点A的坐标及反比例函数的解析式.

（本题6分）在某一电路中，保持电压不变，电流I（安培）与电阻R（欧姆）成反比例．当电阻R=6欧姆时，电流 I=2安培．
（l）求I与R之间的函数关系式；
（2）当电流I="1.5" 安培时，求电阻R的值；
（3）如果电路中用电器限制电流不得超过10安培，那么用电器的可变电阻应控制在什么范围内？

如图，已知A（-4，0．5），B（-1，2）是一次函数y=ax+b与反比例函数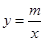（m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．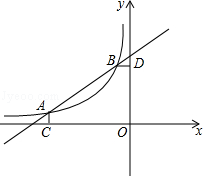 

（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．

已知：正比例函数的图象于反比例函数的图象交于点M（a，1），MN⊥x轴于点N（如图），若△OMN的面积等于2，求这两个函数的解析式．

如图，函数的图象与函数（）的图象交于A（，1）B（1，）两点．

（1）求函数的表达式；    
（2）观察图象，比较当时，与的大小．

如图，A、B是双曲线y=上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C，过B点作BE⊥x轴，垂足为E．若△ADO的面积为1，D为OB的中点，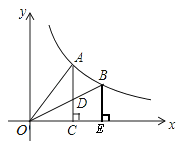

（1）求四边形DCEB的面积。
（2）求k的值。

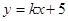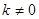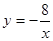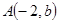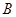如图，一次函数（为常数，且）的图像与反比例函数的图像交于，两点．

（1）求一次函数的表达式；
（2）若将直线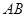向下平移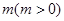个单位长度后与反比例函数的图像有且只有一个公共点，求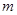的值．

如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴上，函数y=的图象过点P（4，3）和矩形的顶点B（m，n）（0＜m＜4）．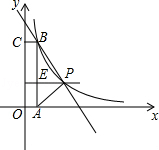

（1）求k的值；
（2）连接PA，PB，若△ABP的面积为6，求直线BP的解析式．

已知函数与函数交于点A（2，b）B（-3，m）两点（点A在第一象限），

（1）求b，m，k的值；
（2）函数 与x轴交于点C，求△ABC的面积．

已知：如图，反比例函数的图象经过点A、B，点A的坐标为（1，3），点B的纵坐标为1，点C的坐标为（2，0）．

（1）求该反比例函数的解析式；
（2）求直线BC的解析式．