已知: 与
与 成正比例,且
成正比例,且 时,
时, 。
。
(1)试求 与
与 之间的函数关系式;
之间的函数关系式;
(2)当 时,求
时,求 的值;
的值;
(3)当 取何值时,
取何值时, ?;
?;
在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有有无数多个.
(1)若点M(2,a)是反比例函数 (k为常数,
(k为常数, )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;
(2)函数 (m为常数,
(m为常数, )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
已知水池的容量一定,当每小时的灌水量为q=3米3时,灌满水池所需的时间为t=12小时.
⑴写出灌水量q与灌满水池所需的时间t的函数关系式;
⑵求当灌满水池所需8小时时,每小时的灌水量.
(本题10分)如图, 的图象与反比例函数
的图象与反比例函数 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
(1)求这两个函数的表达式;
(2)请直接写出当x取何值时, .
.
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图所示,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
已知直线y=﹣3x与双曲线y=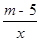 交于点P (﹣1,n).
交于点P (﹣1,n).
(1)求m的值;
(2)若点A ( ,
, ),B(
),B( ,
, )在双曲线y=
)在双曲线y=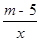 上,且
上,且 <
< <0,试比较
<0,试比较 ,
, 的大小.
的大小.
如图,在直角坐标系中,已知菱形ABCD的面积为15,顶点A在双曲线 上,CD与y轴重合,且AB⊥x轴于B,AB=5.
上,CD与y轴重合,且AB⊥x轴于B,AB=5.
(1)求顶点A的坐标和k的值;
(2)求直线AD的解析式.
某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3。写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式。并给出自变量x的取值范围。
如图,在平面直角坐标系xOy中,直线y=﹣ x+b与x轴交于点A,与双曲线y=﹣
x+b与x轴交于点A,与双曲线y=﹣ 在第二象限内交于点B(﹣3,a).
在第二象限内交于点B(﹣3,a).
(1)求a和b的值;
(2)过点B作直线l平行x轴交y轴于点C,求△ABC的面积.
如图,A、B是双曲线y= 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,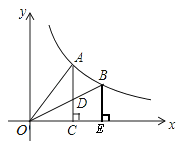
(1)求四边形DCEB的面积。
(2)求k的值。
如图,一次函数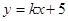 (
( 为常数,且
为常数,且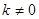 )的图像与反比例函数
)的图像与反比例函数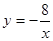 的图像交于
的图像交于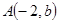 ,
,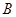 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线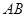 向下平移
向下平移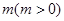 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求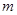 的值.
的值.
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y= 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).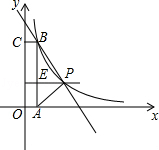
(1)求k的值;
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
已知函数 与函数
与函数 交于点A(2,b)B(-3,m)两点(点A在第一象限),
交于点A(2,b)B(-3,m)两点(点A在第一象限),
|
 与x轴交于点C,求△ABC的面积.
与x轴交于点C,求△ABC的面积.