如图,A、B是双曲线y= 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,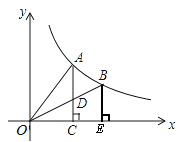
(1)求四边形DCEB的面积。
(2)求k的值。
相关知识点
推荐套卷
如图,A、B是双曲线y= 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
(1)求四边形DCEB的面积。
(2)求k的值。