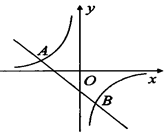
如图,已知反比例函数y=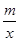 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).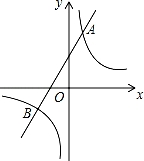
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
已知函数y与x+1成反比例,且当x=﹣2时,y=﹣3.
(1)求y与x的函数关系式;
(2)当x=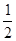 时,求y的值.
时,求y的值.
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数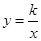 (
( )的图象经过点D且与边BA交于点E,连接DE.
)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为2,则k=;
(2)连接CA,DE与CA是否平行?请说明理由;
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
如图1,点A(8,1)、B(n,8)都在反比例函数 (x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(1)求m的值和直线AB的函数关系式;
(2)动点P从O点出发,以每秒2个单位长度的速度沿折线OD﹣DB向B点运动,同时动点Q从O点出发,以每秒1个单位长度的速度沿折线OC向C点运动,当动点P运动到D时,点Q也停止运动,设运动的时间为t秒.
①设△OPQ的面积为S,写出S与t的函数关系式;
②如图2,当的P在线段OD上运动时,如果作△OPQ关于直线PQ的对称图形△O′PQ,是否存在某时刻t,使得点Q′恰好落在反比例函数的图象上?若存在,求Q′的坐标和t的值;若不存在,请说明理由.
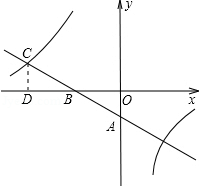
如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y= 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.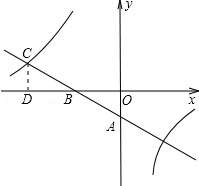
 (1)求一次函数与反比例的解析式;
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣ >0的解集.
>0的解集.
已知一次函数的图象与双曲线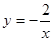 交于两点的坐标分别为(
交于两点的坐标分别为(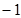 ,
, )、(
)、(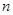 ,-1);
,-1);求该一次函数的解析式
描出函数草图,根据图象写出使一次函数的值大于反比例函数的值的
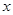 的取值范围.
的取值范围.
如图,在平面直角坐标系xOy中,一次函数y=-2x的图象与反比例函数y= 的图象的一个交点为A(-1,n)
的图象的一个交点为A(-1,n)
求反比例函数y=
 的解析式
的解析式若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
如图,一次函数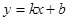 的图像与反比例函数
的图像与反比例函数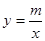 的图像交于
的图像交于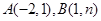 两点。
两点。
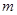 的值;
的值;求一次函数的解析式;
若直线AB交
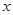 轴于点C,求△OBC的面积
轴于点C,求△OBC的面积根据图象写出使一次函数的值小于反比例函数的值的x的取值范围
将直线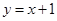 向左平移2个单位后得到直线l,若直线l与反比例函数
向左平移2个单位后得到直线l,若直线l与反比例函数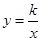 的图象的交点为(2,-m).
的图象的交点为(2,-m).求直线l的解析式及直线l与两坐标轴的交点;
求反比例函数的解析式.
在平面直角坐标中,直角三角板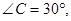
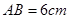 ,将直角顶点
,将直角顶点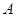 放在点(
放在点( ,1)处,
,1)处,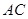 ∥
∥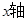 ,求经过点C的反比例函数的解析式.
,求经过点C的反比例函数的解析式.
如图,一次函数y=kx+b图象与反比例函数y=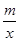 图象交于A(-2,1),B(1,n)两点
图象交于A(-2,1),B(1,n)两点求反比例函数的解析式;
根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
如图,双曲线 上点A的坐标为(1,2),过点A的直线y=x+b交x轴于点M,交y轴于点N,过A作AP⊥x轴于点P。
上点A的坐标为(1,2),过点A的直线y=x+b交x轴于点M,交y轴于点N,过A作AP⊥x轴于点P。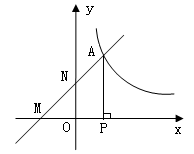
分别求k、b的值;
求△AMP的周长。