如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=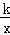 的图象经过点C,一次函数y=ax+b的图象经过点A ,C。
的图象经过点C,一次函数y=ax+b的图象经过点A ,C。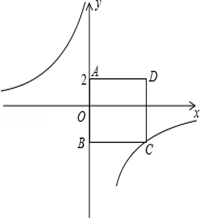
(1)求反比例函数与一次函数的解析式;
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是 .若反比例函数y=
.若反比例函数y= 的图象经过点B,则此反比例函数表达式中的K为 .
的图象经过点B,则此反比例函数表达式中的K为 .

(本小题满分10分)如图,一次函数y1=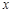 +1的图象与反比例函数
+1的图象与反比例函数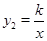 (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当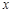 >0时,
>0时,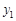 与
与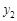 的大小.
的大小.
反比例函数y= 的图象如图所示,以下结论:
的图象如图所示,以下结论:

①常数m<-1;
②在每个象限内,y随x的增大而增大;
③若A(-1,h),B(2,k)在图象上,则h<k;
④若p(x,y)在图象上,则p1(-x,-y)也在图象上.
其中正确的是( )
| A.①② | B.②③ | C.③④ | D.①④ |
下列函数中,当x>0时,y随x增大而减小的是( )
| A.y=x2 | B.y=x-1 | C.y= |
D.y=-x2 |
直线y=- x-1与反比例函数
x-1与反比例函数 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )

| A.-2 | B.-4 | C.-6 | D.-8 |
已知点A(-1,y1)、B(2,y2)都在双曲线 上,则y1、y2的大小关系是( )
上,则y1、y2的大小关系是( )
| A.y1<y2 | B.y1>y2 | C.y1=y2 | D.无法确定 |
已知直线y=kx(k﹥0)与双曲线 交于点A(x1,y1),B(x2,y2)两点,则2x1y2-x2y1的值为:
交于点A(x1,y1),B(x2,y2)两点,则2x1y2-x2y1的值为:
| A.-3 | B.-6 | C.0 | D.3 |
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数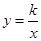 (
( )的图象经过点D且与边BA交于点E,连接DE.
)的图象经过点D且与边BA交于点E,连接DE.
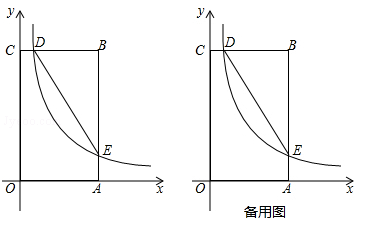
(1)连接OE,若△EOA的面积为2,则k= ;
(2)连接CA,DE与CA是否平行?请说明理由;
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
面积为2的△ABC,一边长为 ,这边上的高为
,这边上的高为 ,则
,则 与
与 的变化规律用图象表示大致是( )
的变化规律用图象表示大致是( )
