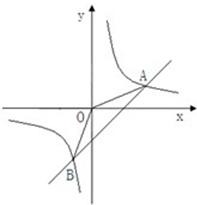
如图, 两点在函数
两点在函数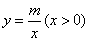 的图象上.
的图象上.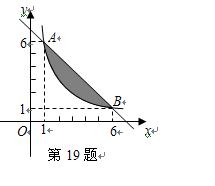
(1).求 的值及直线
的值及直线 的解析式
的解析式
(2).如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,请直接写出图中阴影部分(不包括边界)所含格点的个数.
图中阴影部分(不包括边界)所含格点的个数是 .………………6分
(12分)如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数n的取值范围是什么?
(2)若函数图象经过点(3,1),求n的值;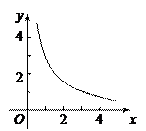 (3)在这个函数图象的某一支上任取点A(a1,b1)和点B(a2,b2),如果a1<a2,试比较b1和b2的大小.
(3)在这个函数图象的某一支上任取点A(a1,b1)和点B(a2,b2),如果a1<a2,试比较b1和b2的大小.
直线 与反比例函数
与反比例函数 的图象相交于点
的图象相交于点 、
、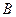 ,
, 与
与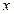 轴交于点
轴交于点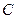 ,其中点
,其中点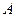 的坐标为
的坐标为 ,点
,点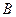 的横坐标为
的横坐标为 .
.
(1)试确定反比例函数的关系式.
(2)求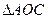 的面积.
的面积.
(3)如图直接写出反比例函数值大于一次函数值的自变量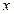 的取值范围.
的取值范围.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数 的图
的图
象交于 ,
, 两点,且点
两点,且点 的横坐标和
的横坐标和 点的纵坐标都是
点的纵坐标都是 .求:
.求:
(1)一次函数解析式;
(2)求 的面积.
的面积.
(3)观察图像,直接写出一次函数值小于反比例函数值的x的取值范围
 |
函数 的图象如图所示.
的图象如图所示.
(1) (
( )是第一象限内图象上的点,且
)是第一象限内图象上的点,且 都是整数.求出所有的点
都是整数.求出所有的点 ;
; (2)若P(m,y1),Q(-3,y2)是函数
(2)若P(m,y1),Q(-3,y2)是函数 图象上的两点,且y1> y2,求实数m的取值范围.
图象上的两点,且y1> y2,求实数m的取值范围.
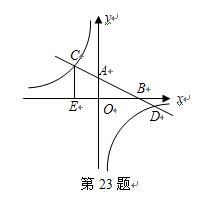
已知:如图,在平面直角坐标系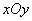 中,直线AB分别与
中,直线AB分别与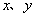 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,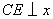 轴于点E,
轴于点E,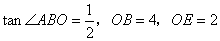 .
.
(1). 求该反比例函数的解析式;
(2). 求直线AB的解析式
如图,已知一次函数y=kx +b的图象与反比例函数
+b的图象与反比例函数
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△ABC的面积.
已知一次函数 与反比例函数
与反比例函数 的图象,有一个交点的纵坐标是2,则
的图象,有一个交点的纵坐标是2,则
b的值为________。
已知点A(x1,y1)、B(x2,y2)在反比例函数y=- 的图象上,且x1<0<x2,则y1、
的图象上,且x1<0<x2,则y1、
y2和0的大小关系( )
| A.y1>y2>0 | B.y1<y2<0 | C.y1>0>y2 | D.y1<0<y2 |
已知: 反比例函数
反比例函数 经过点B(1,1) .
经过点B(1,1) .
(1)求该反比例函数解析式;
(2) 联结OB,再把点
联结OB,再把点 A(2,0)与点B联结,将△OAB绕点O按顺时针方向旋转135°得到△O
A(2,0)与点B联结,将△OAB绕点O按顺时针方向旋转135°得到△O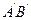 ,写出
,写出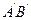 的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m,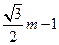 )(其中m>0),在线段OF上任取一点E,
)(其中m>0),在线段OF上任取一点E,
设E点的纵坐标为n,过F点作FM⊥x轴于点M,联结EM,使△OEM的面积是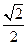 ,求代数式
,求代数式 的值.
的值.
在平面直角坐标系xOy中,一次函数y=k x+b与反比例函数y=
x+b与反比例函数y= 的图象交于
的图象交于
A(1,6),B(a,3)两点.
(1)求k , k
, k 的值;
的值;
(2)如图,点D在x轴上,在梯形OBCD中,BC∥OD,OB=DC,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为18时,求PE:PC的值.
、如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=﹣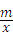 的图象的交点.
的图象的交点.
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.