如图,将等边 绕点 顺时针旋转 得到 ,连接 , .则下列结论:
① ;② ;③四边形 是菱形.
其中正确的个数是
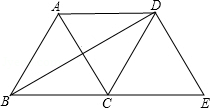
A.0B.1C.2D.3
如图,将
绕边
的中点
顺时针旋转
.嘉淇发现,旋转后的
与
构成平行四边形,并推理如下: 
小明为保证嘉淇的推理更严谨,想在方框中" ,"和" 四边形 "之间作补充,下列正确的是
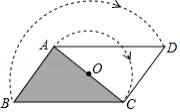
| A. |
嘉淇推理严谨,不必补充 |
B. |
应补充:且 |
| C. |
应补充:且 |
D. |
应补充:且 |
如图, 为等边三角形 内的一点,且 到三个顶点 , , 的距离分别为3,4,5,则 的面积为
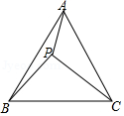
A. B. C. D.
已知正方形 和正六边形 边长均为1,把正方形放在正六边形中,使 边与 边重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点 顺时针旋转,使 边与 边重合,完成第一次旋转;再绕点 顺时针旋转,使 边与 边重合,完成第二次旋转; 在这样连续6次旋转的过程中,点 , 间的距离可能是

| A. |
1.4 |
B. |
1.1 |
C. |
0.8 |
D. |
0.5 |
如图,将矩形 绕点 旋转至矩形 的位置,此时点 恰好与 的中点重合, 交 于点 ,若 ,则 的长为

A.4B. C. D.6
如图,在矩形 中, , 为 边的中点,将 绕点 顺时针旋转 ,点 的对应点为 ,点 的对应点为 ,过点 作 交 于点 ,连接 、 交于点 ,现有下列结论:
① ;
② ;
③ ;
④点 为 的外心.
其中正确的个数为

A.1个B.2个C.3个D.4个
(年新疆、生产建设兵团)如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )

A.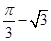 |
B. |
C.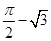 |
D.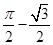 |
(年青海省中考)一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )

| A.105° | B.115° | C.120° | D.135° |
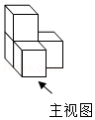
如图是由4个相同的小正方体堆成的物体,将它在水平面内顺时针旋转 后,其主视图是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , , ,将 绕点 逆时针旋转得到 △ ,使点 落在 边上,连接 ,则 的长度是

A. B. C. D.
如图, 中, , .将 绕点 逆时针方向旋转得到△ .此时恰好点 在 上, 交 于点 ,则 与 的面积之比为

A. B. C. D.
如图,在 中, , , ,将 绕点 逆时针旋转,使点 落在线段 上的点 处,点 落在点 处,则 、 两点间的距离为

A. B. C.3D.
如图,将△ ABC绕点 A逆时针旋转55°得到△ ADE,若 且 于点 F,则∠ BAC的度数为( )

| A. |
65° |
B. |
70° |
C. |
75° |
D. |
80° |
如图,在 中, , .将 绕点 逆时针方向旋转 ,得到△ ,连接 .则线段 的长为

| A. |
1 |
B. |
|
C. |
|
D. |
|