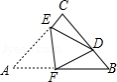
如图,在等边 中,
中, ,点
,点 是
是 边上的动点,点
边上的动点,点 关于直线
关于直线 ,
, 的对称点分别为
的对称点分别为 ,
, ,则线段
,则线段 长的取值范围是 .
长的取值范围是 .

如图,在 中,
中, ,
, ,将
,将 折叠,使点
折叠,使点 落在
落在 边上的点
边上的点 处,
处, 为折痕,若
为折痕,若 ,则
,则 的值为
的值为


A. B. C. D.
如图,在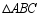 中,
中,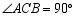 ,
,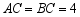 ,将
,将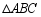 折叠,使点
折叠,使点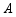 落在
落在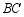 边上的点
边上的点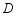 处,
处,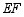 为折痕,若
为折痕,若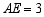 ,则
,则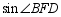 的值为
的值为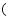
A. B. C. D.
如图,已知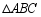 ,
, ,将
,将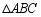 沿边
沿边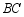 翻转,得到的
翻转,得到的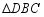 与原
与原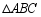 拼成四边形
拼成四边形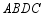 ,则能直接判定四边形
,则能直接判定四边形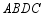 是菱形的依据是
是菱形的依据是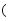

A.一组邻边相等的平行四边形是菱形
B.四条边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相平分的平行四边形是菱形
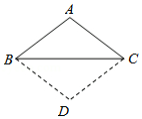
如图,等腰 中,
中,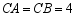 ,
,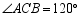 ,点
,点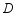 在线段
在线段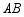 上运动(不与
上运动(不与 、
、 重合),将
重合),将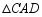 与
与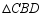 分别沿直线
分别沿直线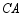 、
、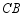 翻折得到
翻折得到 与
与 ,给出下列结论:
,给出下列结论:
①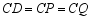 ;
;
②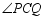 的大小不变;
的大小不变;
③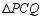 面积的最小值为
;
面积的最小值为
;
④当点 在
在 的中点时,
的中点时, 是等边三角形,
是等边三角形,
其中所有正确结论的序号是 .
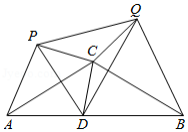
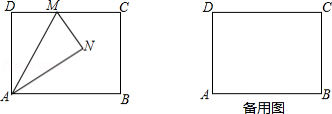
如图,矩形 中,
中,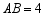 ,
, ,
,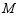 是边
是边 上一点,将
上一点,将 沿直线
沿直线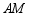 对折,得到
对折,得到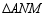 .
.
(1)当 平分
平分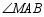 时,求
时,求 的长;
的长;
(2)连接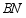 ,当
,当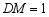 时,求
时,求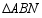 的面积;
的面积;
(3)当射线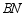 交线段
交线段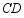 于点
于点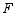 时,求
时,求 的最大值.
的最大值.
如图,矩形纸片  中,
中,  ,
,  ,先按图(2)操作:将矩形纸片
,先按图(2)操作:将矩形纸片  沿过点
沿过点  的直线折叠,使点
的直线折叠,使点  落在边
落在边  上的点
上的点  处,折痕为
处,折痕为  ;再按图(3)操作,沿过点
;再按图(3)操作,沿过点  的直线折叠,使点
的直线折叠,使点  落在
落在  上的点
上的点  处,折痕为
处,折痕为  ,则
,则  、
、  两点间的距离为 .
两点间的距离为 .

如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若 ,∠EFA=60°,则四边形A′B′EF的周长是( )

A.1+3 B.3+ C.4+ D.5+
如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为 cm.

如图,矩形 ABCD中,对角线 , E为 BC边上一点, BC=3 BE,将矩形 ABCD沿 AE所在的直线折叠, B点恰好落在对角线 AC上的 B′处,则 AB= .

如图,已知⊙ O的半径为2, AB为直径, CD为弦. AB与 CD交于点 M,将 沿 CD翻折后,点 A与圆心 O重合,延长 OA至 P,使 AP= OA,连接 PC
(1)求 CD的长;
(2)求证: PC是⊙ O的切线;
(3)点 G为 的中点,在 PC延长线上有一动点 Q,连接 QG交 AB于点 E.交 于点 F( F与 B、 C不重合).问 GE• GF是否为定值?如果是,求出该定值;如果不是,请说明理由.

已知 为 的直径且长为 , 为 上异于 , 的点,若 与过点 的 的切线互相垂直,垂足为 .①若等腰三角形 的顶角为120度,则 ,②若 为正三角形,则 ,③若等腰三角形 的对称轴经过点 ,则 ,④无论点 在何处,将 沿 折叠,点 一定落在直径 上,其中正确结论的序号为 .
如图,把某矩形纸片 沿 , 折叠(点 、 在 边上,点 , 在 边上),使点 和点 落在 边上同一点 处, 点的对称点为 、 点的对称点为 ,若 , , ,则矩形 的长为

| A. |
|
B. |
|
C. |
|
D. |
|