初中数学翻折变换（折叠问题）试题

如图，在矩形 ABCD中， AB＝8， BC＝6， M为 AD上一点，将△ ABM沿 BM翻折至△ EBM， ME和 BE分别与 CD相交于 O， F两点，且 OE＝ OD，则 AM的长为 　　．

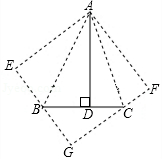
如图，在△ ABC中，∠ BAC＝45°， AD⊥ BC于点 D， BD＝6， DC＝4，求 AD的长．小明同学利用翻折，巧妙地解答了此题，按小明的思路探究并解答下列问题：

（1）分别以 AB， AC所在直线为对称轴，画出△ ABD和△ ACD的对称图形，点 D的对称点分别为点 E， F，延长 EB和 FC相交于点 G，求证：四边形 AEGF是正方形；

（2）设 AD＝ x，建立关于 x的方程模型，求出 AD的长．

如图，将平行四边形 ABCD沿对角线 BD折叠，使点 A落在点 A′处，∠1＝∠2＝48°，则∠ A′的度数为 　 　．

如图，在▱ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若 $\angle B＝52°，\angle \mathit{DAE}＝20°$，则∠FED′的大小为　   　．

如图，将矩形纸片 $\mathit{ABCD}（\mathit{AD}＞\mathit{AB}）$折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F．

（1）判断四边形CEGF的形状，并证明你的结论；

（2）若 $\mathit{AB}＝3，\mathit{BC}＝9$，求线段CE的取值范围．

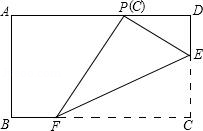
如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC＝3DE＝3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP＝　   　．

如图，菱形ABCD的边AB＝8，∠B＝60°，P是AB上一点，BP＝3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（　　）

A．5B．7C．8D． $\frac{13}{2}$

如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．

（1）求⊙O的半径；

（2）点E为圆上一点，∠ECD＝15°，将 $\stackrel{̂}{\mathit{CE}}$沿弦CE翻折，交CD于点F，求图中阴影部分的面积．

如图，将半圆形纸片折叠，使折痕 CD与直径 AB平行， $\stackrel{⏜}{\mathit{CD}}$ 的中点 P落在 OP上的点 P'处，且 OP'＝ $\frac{1}{3}$ OP，折痕 CD＝2 $\sqrt{3}$ ，则tan∠ COP的值为（　　）

A．

$\frac{6}{5}\sqrt{5}$

B．

$\frac{\sqrt{3}}{2}$

C．

$\frac{\sqrt{5}}{2}$

D．

$\frac{2}{5}\sqrt{5}$

如图，将边长为4的菱形 ABCD纸片折叠，使点 A恰好落在对角线的交点 O处，若折痕 EF＝2 $\sqrt{3}$ ，则∠ A＝（　　）

A．

120°

B．

100°

C．

60°

D．

30°

如图，Rt△ ABC中， AB＝9， BC＝6，∠ B＝90°，将△ ABC折叠，使 A点与 BC的中点 D重合，折痕为 PQ，则线段 BQ的长度为（　　）

A．

$\frac{5}{3}$

B．

$\frac{5}{2}$

C．

4

D．

5

如图，将矩形纸片 ABCD折叠，使点 B与点 D重合，折痕为 MN，若 AB＝2， BC＝4，那么线段 MN的长为（　　）

A．

$\frac{2\sqrt{5}}{5}$

B．

$\sqrt{5}$

C．

$\frac{4\sqrt{5}}{5}$

D．

2 $\sqrt{5}$

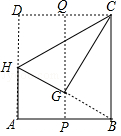
如图，在一张矩形纸片 ABCD中， AB＝3，点 P， Q分别是 AB和 CD的中点，现将这张纸片折叠，使点 D落到 PQ上的点 G处，折痕为 CH，若 HG的延长线恰好经过点 B，则 AD的长为 　　．

如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若 $\mathit{OB}=\sqrt{5}$， $\text{tan}\angle \mathit{BOC}=\frac{1}{2}$,则点A′的坐标为　　．

将一张矩形纸片折叠成如图所示的图形，若AB＝6cm，则AC＝　　cm．