将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 在第一象限, , ,点 在边 上(点 不与点 , 重合).
(Ⅰ)如图①,当 时,求点 的坐标;
(Ⅱ)折叠该纸片,使折痕所在的直线经过点 ,并与 轴的正半轴相交于点 ,且 ,点 的对应点为 ,设 .
①如图②,若折叠后△ 与 重叠部分为四边形, , 分别与边 相交于点 , ,试用含有 的式子表示 的长,并直接写出 的取值范围;
②若折叠后△ 与 重叠部分的面积为 ,当 时,求 的取值范围(直接写出结果即可).

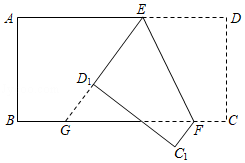
如图,将矩形纸片 沿 折叠后,点 、 分别落在点 、 的位置, 的延长线交 于点 ,若 ,则 等于
| A. |
|
B. |
|
C. |
|
D. |
|
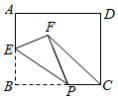
如图,在矩形 中, 为 的中点, 为 边上的任意一点,把 沿 折叠,得到 ,连接 .若 , ,则 的最小值为 .
如图,在 纸片中, , , ,点 , 分别在 , 上,连结 ,将 沿 翻折,使点 的对应点 落在 的延长线上,若 平分 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
(1)如图1,将矩形 折叠,使 落在对角线 上,折痕为 ,点 落在点 处,若 ,则 的度数为 .
(2)小明手中有一张矩形纸片 , , .
【画一画】
如图2,点 在这张矩形纸片的边 上,将纸片折叠,使 落在 所在直线上,折痕设为 (点 , 分别在边 , 上),利用直尺和圆规画出折痕 (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
【算一算】
如图3,点 在这张矩形纸片的边 上,将纸片折叠,使 落在射线 上,折痕为 ,点 , 分别落在点 , 处,若 ,求 的长;
【验一验】
如图4,点 在这张矩形纸片的边 上, ,将纸片折叠,使 落在 所在直线上,折痕为 ,点 , 分别落在点 , 处,小明认为 所在直线恰好经过点 ,他的判断是否正确,请说明理由.

如图,在 中, , , ,将 沿直线 AC翻折至 所在的平面内,得 .过点 A作 ,使 ,与 的延长线交于点 E,连接 BE,则线段 BE的长为( )

| A. |
|
B. |
3 |
C. |
|
D. |
4 |
如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

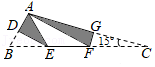
如图,将三角形纸片 ABC折叠,使点 B、 C都与点 A重合,折痕分别为 DE、 FG.已知 , , ,则 BC的长为 .
如图,矩形 中, 是 的中点,将 沿 翻折,点 落在点 处, .设 , 的面积为 ,则 与 的函数图象大致为

A. B.
B.
C.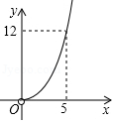 D.
D.
如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
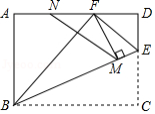
如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
将一张圆形纸片(圆心为点 沿直径 对折后,按图1分成六等份折叠得到图2,将图2沿虚线 剪开,再将 展开得到如图3的一个六角星.若 ,则 的度数为 .

如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .
