初中数学扇形面积的计算填空题

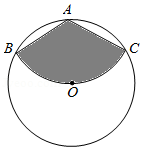
如图，在边长为3的正六边形中，将四边形绕顶点顺时针旋转到四边形处，此时边与对角线重叠，则图中阴影部分的面积是　 　．

若一个扇形的圆心角为，面积为，则这个扇形的弧长为　　（结果保留．

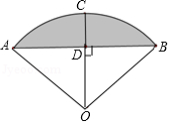
如图，从一块半径为 $1m$ 的圆形铁皮上剪出一个圆周角为 $120°$ 的扇形 $\mathit{ABC}$ ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为 　 　 $m$ ．

如图，半圆的直径，点在半圆上，，则阴影部分的面积为　　（结果保留．

如图，为半圆的直径，且，将半圆绕点顺时针旋转，点旋转到点的位置，则图中阴影部分的面积为　　．

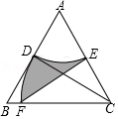
如图，等边三角形的边长为2，以为圆心，1为半径作圆分别交，边于，，再以点为圆心，长为半径作圆交边于，连接，，那么图中阴影部分的面积为　　．

如图，在中，，若将绕点顺时针旋转，点的对应点为点，点的对应点为点，点为的中点，连接．则点的运动路径与线段、围成的阴影部分面积是　　．

《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积（弦矢矢．弧田是由圆弧和其所对的弦围成（如图中的阴影部分），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理（当半径弦时，平分可以求解．现已知弦米，半径等于5米的弧田，按照上述公式计算出弧田的面积为　　平方米．

如图，分别以边长为2的等边三角形的三个顶点为圆心，以边长为半径作弧，三段弧所围成的图形是一个曲边三角形，已知是的内切圆，则阴影部分面积为　　．

如图，，，以点为圆心，为半径作弧交于点、点，交于点，若，则阴影部分的面积为　　．

如图，已知动点在函数的图象上，轴于点，轴于点，延长交以为圆心长为半径的圆弧于点，延长交以为圆心长为半径的圆弧于点，直线分别交轴、轴于点、，当时，图中阴影部分的面积等于　　．

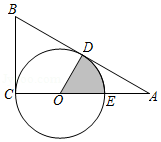
如图，为直角边上一点，以为半径的与斜边相切于点，交于点，已知，．则图中阴影部分的面积是　　．

如图，在平行四边形中，，，，以为直径的交于点，则图中阴影部分的面积为　　．

给出下列结论：

①三角形的重心是三角形三条边上的中线的交点；

②圆内接四边形的对角相等；

③圆心角为，半径为4的扇形的面积是；

④在平面直角坐标系中，如果以原点为位似中心画出一个与原图形位似的图形，它与原图形的相似比为3，那么与原图形上的点对应的位似图形上点的坐标为或．

其中正确的结论是　　（填写正确结论的编号）

如图，四边形是矩形，，，以点为圆心，长为半径画弧，交于点，交的延长线于点，则图中阴影部分的面积是　　．