如图,矩形 中, , ,将此矩形绕点 顺时针方向旋转 得到矩形 ,点 在边 上.
(1)若 , ,求在旋转过程中,点 到点 所经过路径的长度;
(2)将矩形 继续绕点 顺时针方向旋转得到矩形 ,点 在 的延长线上,设边 与 交于点 ,若 ,求 的值.

如图,在 中, ,以 为直径的半圆 交 于点 ,过点 作半圆 的切线,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据: , 取

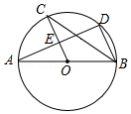
如图,已知 是 的直径, , 是 上的点, ,交 于点 ,连接 .
(1)求证: ;
(2)若 , ,求 的长.
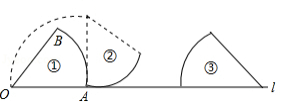
如图,放置在直线 上的扇形 .由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径 , ,则点 所经过的运动路径的长是
A. B. C. D.
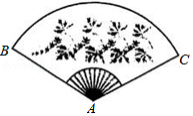
如图,扇形纸扇完全打开后,外侧两竹条 , 的夹角为 , 长为30厘米,则 的长为 厘米.(结果保留
如图,在扇形 中, , 平分 交 于点 ,点 为半径 上一动点.若 ,则阴影部分周长的最小值为 .

抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图, , 分别与 相切于点 , ,延长 , 交于点 .若 , 的半径为 ,则图中 的长为 .(结果保留

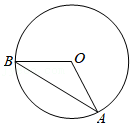
如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, ,对角线 , 经过点 , ,与 交于点 ,连接 并延长与 交于点 ,与 的延长线交于点 , .
(1)求证: 是 的切线;
(2)若 ,求 的长(结果保留 .

如图, 的半径是2,扇形 的圆心角为 .若将扇形 剪下围成一个圆锥,则此圆锥的底面圆的半径为 .
