如图,为
的直径,
为
上一点,过
点的切线交
的延长线于点
,
为弦
的中点,
,
,若点
为直径
上的一个动点,连接
,当
是直角三角形时,
的长为 .

如图,在平面直角坐标系中,已知 ,以点 为圆心的圆与 轴相切.点 、 在 轴上,且 .点 为 上的动点, ,则 长度的最大值为 .

如图,为
的直径,点
为
延长线上的一点,过点
作
的切线
,切点为
,过
、
两点分别作
的垂线
、
,垂足分别为
、
,连接
,则下列结论正确的是 .(写出所有正确结论的序号)
①平分
;
②;
③若,
,则
的长为
;
④若,
,则有
.

如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点
,它们的半径分别为1,2,3,
,按照“加1”依次递增;一组平行线,
,
,
,
,
都与
轴垂直,相邻两直线的间距为1,其中
与
轴重合.若半径为2的圆与
在第一象限内交于点
,半径为3的圆与
在第一象限内交于点
,
,半径为
的圆与
在第一象限内交于点
,则点
的坐标为
为正整数)

如图,为
直角边
上一点,以
为半径的
与斜边
相切于点
,交
于点
,已知
,
.则图中阴影部分的面积是 .
如图,在中,
.
的半径为2,点
是
边上的动点,过点
作
的一条切线
(点
为切点),则线段
长的最小值为 .

如图,在中,
,
,
,点
是
的中点,以
为直径作
,
分别与
,
交于点
,
,过点
作
的切线
,交
于点
,则
的长为 .

如图,已知的半径为2,
为
外一点,过点
作
的一条切线
,切点是
,
的延长线交
于点
,若
,则劣弧
的长为 .

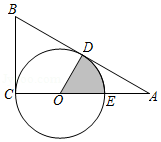
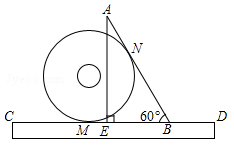
(年贵州省贵阳市)小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .
(年贵州省黔南州)如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是 .
