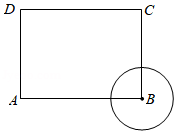
如图,长方形 中, , ,圆 半径为1,圆 与圆 内切,则点 、 与圆 的位置关系是
| A. |
点 在圆 外,点 在圆 内 |
B. |
点 在圆 外,点 在圆 外 |
| C. |
点 在圆 上,点 在圆 内 |
D. |
点 在圆 内,点 在圆 外 |
在 中,若 为 边的中点,则必有: 成立.依据以上结论,解决如下问题:如图,在矩形 中,已知 , ,点 在以 为直径的半圆上运动,则 的最小值为

A. B. C.34D.10
如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 、 与 轴分别交于 、 两点,若点 、点 关于原点 对称,则 的最小值为
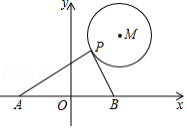
A.3B.4C.6D.8
如图,在网格(每个小正方形的边长均为 中选取9个格点(格线的交点称为格点),如果以 为圆心, 为半径画圆,选取的格点中除点 外恰好有3个在圆内,则 的取值范围为
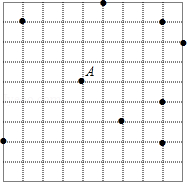
A. B. C. D.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以 为圆心, 为半径画圆,选取的格点中除点 外恰好有3个在圆内,则 的取值范围为
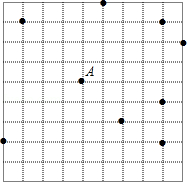
A. B. C. D.
在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
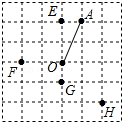
A.E、F、GB.F、G、HC.G、H、ED.H、E、F
平面内,⊙ O的半径为1,点 P到 O的距离为2,过点 P可作⊙ O的切线条数为( )
| A. |
0条 |
B. |
1条 |
C. |
2条 |
D. |
无数条 |
如图,抛物线 与 轴交于 、 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是

| A. |
3 |
B. |
|
C. |
|
D. |
4 |
如图, 在 中, , , ,点 在边 上, , 的半径长为 3 , 与 相交, 且点 在 外, 那么 的半径长 的取值范围是

| A. |
A . B . C . D . |