(1)方法选择
如图①,四边形是
的内接四边形,连接
,
,
.求证:
.
小颖认为可用截长法证明:在上截取
,连接
小军认为可用补短法证明:延长至点
,使得
请你选择一种方法证明.
(2)类比探究
[探究1]
如图②,四边形是
的内接四边形,连接
,
,
是
的直径,
.试用等式表示线段
,
,
之间的数量关系,并证明你的结论.
[探究2]
如图③,四边形是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式是
.
(3)拓展猜想
如图④,四边形是
的内接四边形,连接
,
.若
是
的直径,
,则线段
,
,
之间的等量关系式是 .

如图,点
为线段
的中点,点
,
,
到点
的距离相等,若
,则
的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
给出下列结论:
①三角形的重心是三角形三条边上的中线的交点;
②圆内接四边形的对角相等;
③圆心角为,半径为4的扇形的面积是
;
④在平面直角坐标系中,如果以原点为位似中心画出一个与原图形位似的图形,它与原图形的相似比为3,那么与原图形上的点对应的位似图形上点
的坐标为
或
.
其中正确的结论是 (填写正确结论的编号)
如图,四边形 是 的内接四边形, .若 , ,则下列等式成立的是

| A. |
|
B. |
|
C. |
|
D. |
|
在中,
,
.点
是平面内不与点
,
重合的任意一点.连接
,将线段
绕点
逆时针旋转
得到线段
,连接
,
,
.
(1)观察猜想
如图1,当时,
的值是 ,直线
与直线
相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出
的值及直线
与直线
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点
,
分别是
,
的中点,点
在直线
上,请直接写出点
,
,
在同一直线上时
的值.
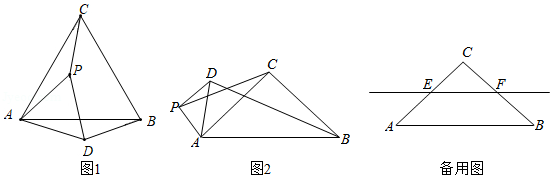
如图,在 中, ,点 是 的中点,以 为直径作 分别交 , 于点 , .
(1)求证: ;
(2)填空:
①若 ,当 时, ;
②连接 , ,当 的度数为 时,四边形 是菱形.

如图, 内接于圆 ,且 ,延长 到点 ,使 ,连接 交圆 于点 .
(1)求证: ;
(2)填空:
①当 的度数为 时,四边形 是菱形.
②若 , ,则 的长为 .

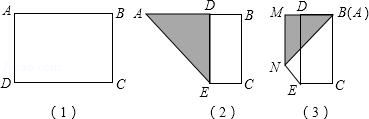
有一张长方形纸片ABCD,如图(1),将它折叠,使AD边落在AB边上,折痕为AE,如图(2);再将∠A折叠,使点A与点B重合,折痕为MN,如图(3).如果AD=4cm,MD=1cm,那么DB= cm.
若一个多边形的内角和为1080°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |