如图，在四边形ABCD中，∠B=∠D，∠1=∠2，求证：四边形ABCD是平行四边形．
已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：
（1）当t为何值时，四边形APFD是平行四边形？
（2）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S四边形APFE：S菱形ABCD=17：40？若存在，求出t的值，并求出此时P，E两点间的距离；若不存在，请说明理由．
如图，已知四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接DE，BF．求证：四边形DEBF是平行四边形．
如图，点E，F分别在正方形ABCD的边DA，DC延长线上，且AE﹣CF，连接BE，BF，过点E作EG∥BF，过点F作FG∥BE，EG，FG交于点G．
（1）求证：△ABE≌△CBF；
（2）求证：四边形BEGF是菱形；
（3）若AD=3AE=3，求四边形BEGF的周长．
如图，四边形ABCD是菱形，CE⊥AB，垂足为点E，且CE交对角线BD于点F．若∠A=120°，四边形AEFD的面积为
，求EF的值．
（1）知识再现
如图（1）：若点A，B在直线l同侧，A，B到l的距离分别是3和2，AB=4，现在直线l上找一点P，使AP+BP的值最小，做法如下；
作点A关于直线l的对称点A′，连接BA′，与直线l的交代就是所求的点P，线段BA′的长度即为AP+BP的最小值，请你求出这个最小值．
（2）实践应用
①如图（2），⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是 ；
②如图（3），Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，
），点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为 ；
③如图（4），菱形ABCD中AB=2，∠A=120°，点P，Q，K，分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为 ；
④如图（5），在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=
，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 ．
（3）拓展延伸
如图（6），在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD，保留作图痕迹，不必写出作法．
（如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．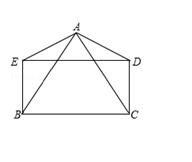
求证：四边形BCDE是矩形．
如图，在平行四边形ABCD中，E、F分别是CD，AB上的点，且DE=BF，求证：
（1）CE=AF；
（2）四边形AFCE是平行四边形．
如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4；
（1）求证：四边形ACED是平行四边形
（2）求四边形ACEB的周长．
如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．
（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求△BDE的面积．
对于边长为3的正方形ABCD，建立适当的直角坐标系，写出各个顶点的坐标．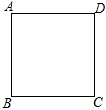
如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5
，且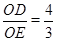
，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=－
+c经过点E，且与AB边相交于点F．
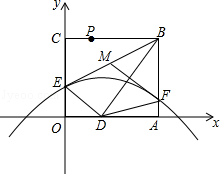
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．
）
粤公网安备 44130202000953号