初中数学圆内接四边形的性质解答题

如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A₁C₁D₁．

（1）证明：△A₁AD₁≌△CC₁B；
（2）若∠ACB=30°，试问当点C₁在线段AC上的什么位置时，四边形ABC₁D₁是菱形．（直接写出答案）

如图，平行四边形ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F。求证：四边形AECF是平行四边形。

如图，△ABC中，AB=AC，AD是△ABC外角的平分线，已知∠BAC=∠ACD．

（1）求证：△ABC≌△CDA；
（2）若∠B=60°，求证：四边形ABCD是菱形．

已知：如图，平行四边形ABCD中，E、F分别是边BC和AD上的点，且BE=DF，求证：AE=CF.

如图，在菱形ABCD中，P是对角线AC上的一点，且PA=PD，⊙O为△APD的外接圆．

（1）试判断直线AB与⊙O的位置关系，并说明理由；
（2）若AC=8，tan∠DAC=，求⊙O的半径．

如图，在梯形中，，．求的长．

如图，▱ABCD中，点E、F分别在AD、BC上，且AE=CF．求证：BE=DF．

如图，在□ABCD中，E、F分别在AD、BC边上，且AE=CF．请你猜想BE与DF的关系，并说明理由．

如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．

（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．

如图，在平面直角坐标系中，AD＝8，OD＝OB，□ABCD的面积为24，求平行四边形的4个顶点的坐标．

（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形（尺规作图，保留作图痕迹），并猜想BE与CD的关系：___________；你是通过证明_______________ 得到的。
（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？并说明理由；
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．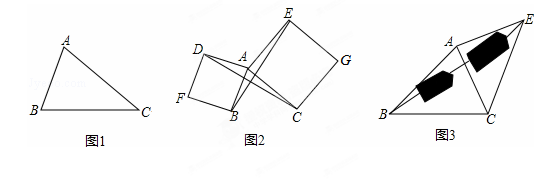

如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．

（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求△BDE的面积．

如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：
（1）在图①中画一条线段MN，使MN=；
（2）在图②中画一个△ABC，使其三边长分别为3，，．

如图，在平行四边形ABCD中，AE=CF，求证：AF=CE．

把一副三角板如图(1)放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=12cm，DC=14cm，把三角板DCE绕点C逆时针旋转15°得到△（如图2）．这时AB与相交于点O，与相交于点F．

（1）填空：∠=     °；
（2）请求出△的内切圆半径；
（3）把△绕着点C逆时针再旋转度（）得△，若△为等腰三角形，求的度数（精确到0.1°）．