如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1．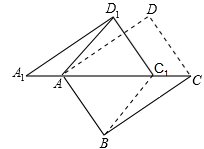
（1）证明：△A1AD1≌△CC1B；
（2）若∠ACB=30°，试问当点C1在线段AC上的什么位置时，四边形ABC1D1是菱形．（直接写出答案）
，求分式
的值：
，试求
的值
相关知识点
推荐套卷
如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1．
（1）证明：△A1AD1≌△CC1B；
（2）若∠ACB=30°，试问当点C1在线段AC上的什么位置时，四边形ABC1D1是菱形．（直接写出答案）
粤公网安备 44130202000953号