把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12cm,DC=14cm,把三角板DCE绕点C逆时针旋转15°得到△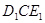 (如图2).这时AB与
(如图2).这时AB与 相交于点O,与
相交于点O,与 相交于点F.
相交于点F.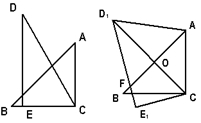
(1)填空:∠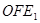 = °;
= °;
(2)请求出△ 的内切圆半径;
的内切圆半径;
(3)把△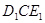 绕着点C逆时针再旋转
绕着点C逆时针再旋转 度(
度( )得△
)得△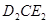 ,若△
,若△ 为等腰三角形,求
为等腰三角形,求 的度数(精确到0.1°).
的度数(精确到0.1°).
相关知识点
推荐套卷
把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12cm,DC=14cm,把三角板DCE绕点C逆时针旋转15°得到△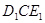 (如图2).这时AB与
(如图2).这时AB与 相交于点O,与
相交于点O,与 相交于点F.
相交于点F.
(1)填空:∠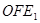 = °;
= °;
(2)请求出△ 的内切圆半径;
的内切圆半径;
(3)把△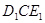 绕着点C逆时针再旋转
绕着点C逆时针再旋转 度(
度( )得△
)得△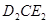 ,若△
,若△ 为等腰三角形,求
为等腰三角形,求 的度数(精确到0.1°).
的度数(精确到0.1°).