已知平行四边形ABCD中,∠B=4∠A,则∠C=( )

| A.18° | B.36° | C.72° | D.144° |
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 .
.
以上结论中,你认为正确的有( )个.
| A.1 | B.2 | C.3 | D.4 |
如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于O, E为DC的一点,过点O作OF⊥OE交BC于F,记 ,则关于d的正确的结论是( )
,则关于d的正确的结论是( )
A. |
B. |
C. |
D. |
如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.

| A.90° | B.30° | C.60° | D.45° |
如图,小亮从A点出发前进10m,向右转一角度,再前进10m,又向右转一相同角度,…,这样一直走下去,他回到出发点A时,一共走了180m,则他每次转动的角度是( )
| A.15° | B.18° | C.20° | D.不能确定 |

如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )

A.四边形ABCD是梯形
B.四边形ABCD是菱形
C.对角线AC=BD
D.AD=BC
如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( ).

| A.①② | B.①③ | C.①②④ | D.①③④ |
如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为
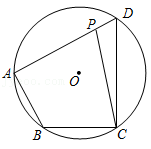
| A. |
|
B. |
|
C. |
|
D. |
|
如图,△ABC中,边BC=12cm,高AD=6cm ,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )

A.3cm B.4cm C.5cm D.6cm
一个多边形的内角和是900°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |
如图所示,菱形ABCD中,对角线相AC、BD交于点O,H为边AD的中点,菱形ABCD的周长为36,则OH的长等于( )

A.4.5 B.5 C.6 D.9
如图,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是()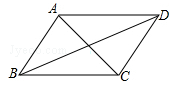
| A.AB=CD |
| B.当AC⊥BD时,它是菱形 |
| C.AB=AC |
| D.当∠ABC=90°时,它是矩形 |
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G,H,则下列结论错误的是( )
(A) (B)
(B) (C)
(C) (D)
(D)