山东省泰安市新泰市八年级下学期期末数学试卷
在实数:3.14159, ,1.010010001…(每相隔1个就多1个0),
,1.010010001…(每相隔1个就多1个0), ,π,
,π, 中,无理数的个数有( ).
中,无理数的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
若x>y,则下列式子中错误的是( ).
| A.x﹣3>y﹣3 | B. |
C.x+3>y+3 | D.﹣3x>﹣3y |
若平行四边形的一边长为2,面积为 ,则此边上的高介于( ).
,则此边上的高介于( ).
| A.3与4之间 | B.4与5之间 | C.5与6之间 | D.6与7之 |
当a为( )值时,不等式a(x﹣3)<2(a﹣x)的解集为x<4.
| A.a=8 | B.a=﹣8 | C.a<8 | D.a>﹣8 |
若x﹣y= -1,xy=
-1,xy= ,则代数式(x﹣1)(y+1)的值等于( ).
,则代数式(x﹣1)(y+1)的值等于( ).
A.2 +2 +2 |
B.2 -2 -2 |
C.2 |
D.2 |
下列说法正确的是( ).
| A.6的平方根是±3 |
| B.﹣3是(﹣3)2的算术平方根 |
C. 是 是 的算术平方根 的算术平方根 |
| D.8的立方根是±2 |
在算式(-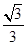 )□(-
)□(-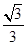 )的□中填上运算符号,使结果最大,这个运算符号是( ).
)的□中填上运算符号,使结果最大,这个运算符号是( ).
| A.加号 | B.减号 | C.乘号 | D.除号 |
实数a在数轴上的位置如图所示,则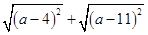 化简后为( ).
化简后为( ).
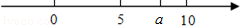
| A.7 | B.﹣7 | C.2a﹣15 | D.无法确定 |
在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,﹣2)处,则此平移可以是( ).
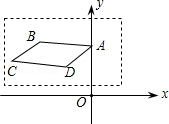
| A.先向右平移5个单位,再向下平移1个单位 |
| B.先向右平移5个单位,再向下平移3个单位 |
| C.先向右平移4个单位,再向下平移4个单位 |
| D.先向右平移4个单位,再向下平移3个单位 |
在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
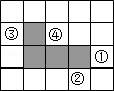
| A.① | B.② | C.③ | D.④ |
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=22°,则∠B的度数是( ).

| A.67° | B.62° | C.82° | D.72° |
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( ).
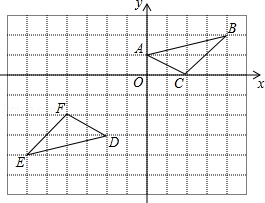
| A.(﹣1,0) | B.(﹣1,﹣1) | C.(﹣2,﹣1) | D.(﹣2,0) |
已知点M(1﹣2m,m﹣1)关于x轴的对称点在第二象限,则m的取值范围在数轴上表示正确的是( ).
A. |
B. |
C. |
D. |
若关于x的一元一次不等式组 有解,则m的取值范围为( ).
有解,则m的取值范围为( ).
A.m< |
B.m≥ |
C.m≤ |
D.m> |
某超市新进一批T恤衫,每件进价为120元,标价为180元,为了促销,超市决定打折销售,但要保证打折后利率不低于20%,则打折后的标价不低于原标价的( )%.
| A.80 | B.90 | C.60 | D.70 |
已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示:
| x |
-2 |
-1 |
0 |
| y |
3 |
2 |
1 |
则不等式kx+b<bx+k的解集为( ).
A.x>﹣1 B.x<1 C.x>﹣3 D.x>1
如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当∠ACB为( )度时,四边形ABFE为矩形.

| A.90° | B.30° | C.60° | D.45° |
已知a、b为有理数,m、n分别表示5﹣ 的整数部分和小数部分,且am+bn(n+2
的整数部分和小数部分,且am+bn(n+2 )=4,则a+b的值为( ).
)=4,则a+b的值为( ).
| A.2 | B.1.5 | C.1 | D.4 |
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
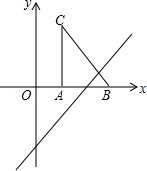
A.80 B.88 C.96 D.100
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客又一次乘出租车的车费为42元,则这位乘客乘车的里程为 km.

如图,将周长为10的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为 .
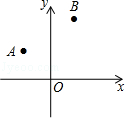
如图,在平面直角坐标系中,点A、B的坐标分别为(﹣1,2)、(1,4),欲在x轴上找一点P,使PA+PB最短,则点P的坐标为 .
小王每天从某报社以每份0.6元买进报纸300份,然后以每份1元卖给读者,报纸卖不完,当天可退回报社,但报社只按每份0.3元退给小王,如果小王平均每天卖出报纸x份,纯收入为y元.
(1)求y与x之间的函数关系式(要求写出自变量x的取值范围);
(2)如果每月以30天计算,小王每天至少要卖多少份报纸(假设小王每天所卖报纸份数相同)才能保证每月收入不低于2600元?
在直角坐标系中,四边形ABCD顶点的位置如图所示.
(1)求边AB,BC,CD,AD的长;
(2)求四边形ABCD的面积.
如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.

(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
 的结果是( ).
的结果是( ). ﹣2
﹣2
 ,则x的取值范围为 .
,则x的取值范围为 . ;
; ,并指出它的所有的非负整数解.
,并指出它的所有的非负整数解. x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号