如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.
(1)若点E平分线段PF,则此时AQ的长为多少?
(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?
(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.

如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半.这样的图形有
图① 图② 图③ 图④
| A.4个 | B.3个 | C.2个 | D.1个 |
在正方形 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,连接
,连接 ,其中
,其中 交直线
交直线 于点
于点 .
.
(1)依题意补全图1;
(2)若 ,求
,求 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.

【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.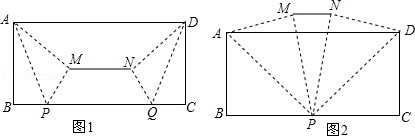
【规律探索】
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
【解决问题】
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
在图1至图4中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE和AD在同一直线上.
操作示例:
当AE<a时,如图1,在BA上选取适当的点G,BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置,恰能构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上,连接CH.由剪拼方法可得DH=BG,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图所示),
实践探究:
(1)小明判断出四边形FGCH是正方形,请你给出判断四边形FGCH是正方形的方法。
(2)经测量,小明发现图1中BG是AE一半,请你证明小明的发现是正确的。(提示:过点F作FM⊥AH,垂足为点M);
拓展延伸
类比图1的剪拼方法,请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图
(本题12分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.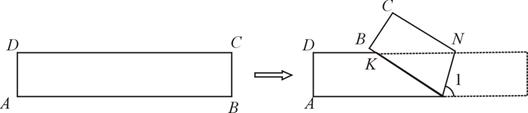
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.
(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.
(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____度时,图中阴影部分的面积和有最大值是________.
如图,在△ABC中,AB=5,AC=9,S△ABC=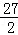 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.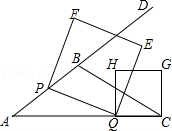
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
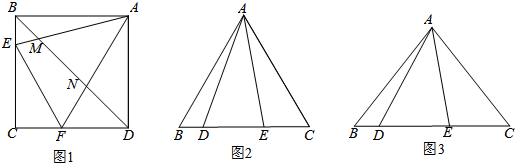
(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足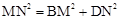 ,请证明这个等量关系;
,请证明这个等量关系;
(2)在△ABC中, AB=AC,点D、E分别为BC边上的两点.
①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;
②如图3,当∠BAC= ,(0°<
,(0°< <90°),∠DAE=
<90°),∠DAE= 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: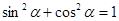 】
】
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为 
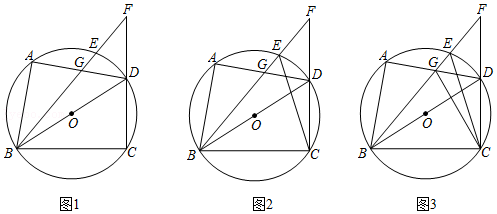
如图1,四边形 内接于 , 为直径, 上存在点 ,满足 ,连结 并延长交 的延长线于点 , 与 交于点 .
(1)若 ,请用含 的代数式表示 .
(2)如图2,连结 , .求证: .
(3)如图3,在(2)的条件下,连结 , .
①若 ,求 的周长.
②求 的最小值.
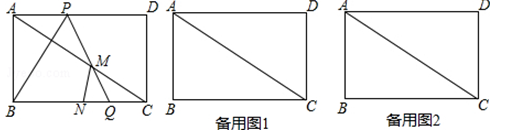
如图1,矩形ABCD中,AB=2 ,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
(1)填空:①∠ACB= 度;②PQ= .
(2)设线段BC的中点为N,PQ与线段AC相交于点M,若△CMN为直角三角形,请直接写出满足条件的AP的长度.
(3)设AP=x,△PBQ与△ABC的重叠部分的面积为S,试求S与x的函数关系式和自变量x的取值范围.
(本题8分)如图,在□ABCD中, 、
、 是
是 、
、 的中点,
的中点, 、
、 的延长线分别交
的延长线分别交 、
、 的延长线于
的延长线于 、
、 ;
;
(1)求证:BH=AB;
(2)若四边形 为菱形,试判断
为菱形,试判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形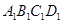 ,
,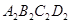 ,
,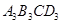 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形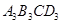 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.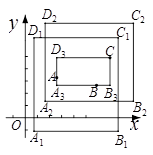
(1)如图1,已知A(-2,0),B(4,3),C(0,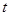 ).
).
①若 ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则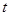 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(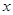 ,
,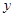 )是抛物线
)是抛物线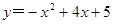 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标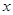 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(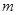 ,
,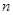 )是函数
)是函数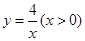 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.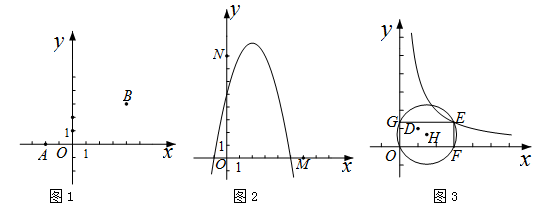
菱形ABCD的对角线AC,BD相交于点O, .动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为
.动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为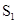 ,未盖住部分的面积为
,未盖住部分的面积为 ,
, .
.
(1)用含x代数式分别表示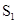 ,
, ;
;
(2)若 ,求x.
,求x.