安徽省淮北市九年级下学期五校联考五数学试卷
2014政府工作报告指出,今年拟安排财政赤字13500亿元,13500亿元用科学记数法可表示为( )
| A.1.35×1011元 | B.0.135×1012元 |
| C.1.35×1012元 | D.13.5×1011元 |
如图,已知a∥b,小明把三角板的直角顶点放在直线b上.若∠2=40°,则∠1的度数为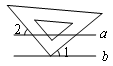
| A.40° | B.35° | C.50° | D.45° |
已知线段AB=16cm,O是线段AB上一点,M是AO的中点,N是BO的中点,则MN=( )
| A.10cm | B.6cm | C.8cm | D.9cm |
在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为 ,则袋中球的总数为( )
,则袋中球的总数为( )
| A.3个 | B.6个 | C.9个 | D.12个 |
把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
| A.m>1 | B.m<-5 | C.-5<m<1 | D.m<1 |
如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在Y轴,X轴上,以AB为弦的⊙M与X轴相切,若点A的坐标为(0,8),则圆心M的坐标为( )
A.(4,-5) B.(5,-4) C.(-5,4) D.(-4,5)
如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )

如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是 .
如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC请你,添加一个条件,使得△ABC和△DEC全等。并加以证明。你添加的条件是 
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-3,3),点C的坐标为(-3,1)。
(1)将Rt△ABC沿x轴正方向平移7个单位得到Rt△A1B1C1,试在图上画出的图形Rt△A1B1C1的图形;
(2)Rt△ABC关于点D(-1,0)对称的图形是Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形,并写出A2、B2、C2点的坐标。
如图,每个大正方形是由边长为1的小正方形组成。观察以上图形,完成下列填空:
(1)猜想:当n为奇数时,图n中黑色小正方形的个数为 ,当n为偶数时,图n中黑色小正方形的个数为 ;
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长。
某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据: )
)
临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元..经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,该店每天可售出 只粽子,利润为 元。
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
我校数学兴趣小组为了解美利达自行车的销售情况,对我市美利达专卖店第一季度 A、B、C、D四种型号的销量做了统计,绘制成如下两幅统计图(均不完整)。
(1) 该店第一季度售出美利达自行车共多少辆?
(2) 把两幅统计图补充完整;
(3) 若该专卖店计划订购这四款型号自行车900辆,求C型自行车应订购多少辆?
如图,抛物线y=ax2 + bx + c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3)。
(1)求抛物线y= ax2 + bx + c 的解析式;
(2)求△AOC和△BOC的面积比;
(3)在对称轴上是否存在一个P点,使△PAC的周长最小。若存在,请你求出点P的坐标;若不存在,请你说明理由。
在图1至图4中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE和AD在同一直线上.
操作示例:
当AE<a时,如图1,在BA上选取适当的点G,BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置,恰能构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上,连接CH.由剪拼方法可得DH=BG,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图所示),
实践探究:
(1)小明判断出四边形FGCH是正方形,请你给出判断四边形FGCH是正方形的方法。
(2)经测量,小明发现图1中BG是AE一半,请你证明小明的发现是正确的。(提示:过点F作FM⊥AH,垂足为点M);
拓展延伸
类比图1的剪拼方法,请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图
 的数是 ( )
的数是 ( ) 


 的值在( )
的值在( ) = .
= . 的解集是 .
的解集是 . ,则OD= .
,则OD= .
 ﹣1)÷
﹣1)÷ ,其中x=2sin60°+1.
,其中x=2sin60°+1. 粤公网安备 44130202000953号
粤公网安备 44130202000953号