初中数学圆内接四边形的性质试题

（本小题12分） 菱形ABCD的边长为2，∠BAD＝60°，对角线AC，BD相交于点O，动点P在线段AC上从点A向点C运动，过P作PE∥AD，交AB于点E，过P作PF∥AB，交AD于点F，四边形QHCK与四边形PEAF关于直线BD对称. 设菱形ABCD被这两个四边形盖住部分的面积为S₁，AP＝x：

（1）对角线AC的长为     ；S_菱形ABCD＝     ；
（2）用含x的代数式表示S₁；
（3）设点P在移动过程中所得两个四边形PEAF与QHCK的重叠部分面积为S₂，当S₂＝S_菱形ABCD时，求x的值．

已知直角坐标系中菱形ABCD的位置如图所示，C．D两点的坐标分别为 （4，0）、（0，3）．现有两动点P、Q分别从A、C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为ts．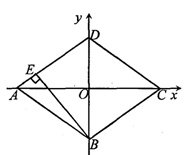

（1）菱形ABCD的边长是   ，面积是   ， 高BE的长是   ．（直接填写结果）
（2）探究下列问题：
①若点P的速度为1cm/s，点Q的速度为2 cm/s．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；
②若点P的速度为1cm/s，点Q的速度变为kcm/s，在运动过程中，任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形，请探究当t＝4s时的情形，并求出k的值．

（本题6分）矩形纸片ABCD中，AB=5，AD=4．

（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是             ；（不必说明理由）
（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．

如图，P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若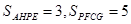，则为 （   ）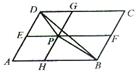

A．0．5  B．1  C．1．5  D．2

如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．

（1）已知：DE∥AC，DF∥BC．
①判断
四边形DECF一定是什么形状？并说明理由．
②裁剪
当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；
（2）折叠
请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．

在□ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．

如图，等腰梯形ABCD中，AB＝CD，AD∥BC，点E、F在BC上，且BE＝CF．

（1）求证：AE＝DF；
（2）若AD＝EF，试证明四边形AEFD为矩形．

矩形ABCD中，边长AB=4，边BC=2，M、N分别是边BC、CD上的两个动点，且始终保持AM⊥MN．则CN的最大为（ ）

A．1           B．       C．      D．2

已知矩形纸片ABCD中，AB=24厘米，BC=10厘米．

（1）按如下操作：先将矩形纸片上下对折，而后左右对折，再沿对角线对折，而后展开得到图中的折痕四边形EFGH（如图1），求菱形EFGH的面积．
（2）如图2，将矩形纸片ABCD折叠，使点A与点C重合得折痕EF，则四边形AECF必为菱形，请加以证明．
（3）请通过一定的操作，构造一个菱形EFGH（不同于第（1）题中的特殊图形），使菱形的四个顶点分别落在矩形ABCD的四条边上（E、F、G、H分别在边AB、BC、CD、DA上，且不与矩形ABCD的顶点重合）．
①请简述操作的方法，并在图3中画出菱形EFGH．
②求菱形EFGH的面积的取值范围．

如图，正方形ABCD的边长为3，点E，F分别在边AB、BC上，AE=BF=1，小球P从点E出发沿直线EF向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P所经过的路程长为（ ）

A．12           B．9             C．4          D．6 

如图①，②在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个     三角形。
（2）如图③，在矩形ABCD中，AB=2，BC=4，，当它的“折痕△BEF”的顶点E位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；
（3）如图④，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？
 
          

如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为      ．

如图，四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂，如此进行下去，得到四边形A_nB_nC_nD_n．
①四边形A₄B₄C₄D₄是菱形；
②四边形A₃B₃C₃D₃是矩形；
③四边形A₇B₇C₇D₇周长为；
④四边形A_nB_nC_nD_n面积为．
上述结论正确的是（     ）

A．①②③

B．②③④

C．①③④

D．①②③④

如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图所示，则△ABC的面积是 （    ）

A．20             B．18             C．16             D．10

如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

（1）试说明四边形EFCG是矩形；
（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．