如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是 .
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
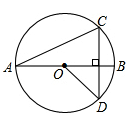
| A.120° | B.140° | C.150° | D.160° |
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
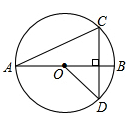
| A.120° | B.140° | C.150° | D.160° |
如图,△ABC内接于⊙O,∠B=60º,∠A=40º,半径OE⊥AB,连接CE,则∠E=( )

| A.5º | B.10º | C.15º | D.20º |
如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
| A. |
|
B. |
|
C. |
|
D. |
|
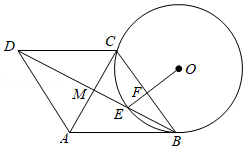
如图,在菱形 中,对角线 、 相交于点 , 经过点 , ,交对角线 于点 ,且 ,连接 交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求 的半径.
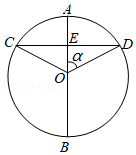
如图, 中,点 为弦 中点,连接 , , ,点 是 上任意一点,则 度数为
| A. |
|
B. |
|
C. |
|
D. |
|
学习圆的性质后,小铭与小熹就讨论起来,小铭说:"被直径平分的弦也与直径垂直",小熹说:"用反例就能说明这是假命题".下列判断正确的是
| A. |
两人说的都对 |
| B. |
小铭说的对,小熹说的反例不存在 |
| C. |
两人说的都不对 |
| D. |
小铭说的不对,小熹说的反例存在 |
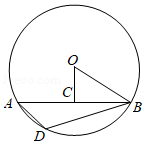
如图, 是 的直径,弦 于点 ,连结 , .若 的半径为 , ,则下列结论一定成立的是
| A. |
|
B. |
|
| C. |
|
D. |
|
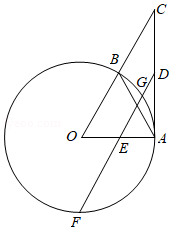
如图,已知 是 的直径, 是 所对的圆周角, .
(1)求 的度数;
(2)过点 作 ,垂足为 , 的延长线交 于点 .若 ,求 的长.

如图, , 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 , 分别是 , 的中点, 所在直线交 于点 , , ,求 的长.