初中数学圆试题

如图，P是矩形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S₁、S₂、S₃、S₄，给出如下结论：
①S₁+S₂=S₃+S₄              ② S₂+S₄= S₁+ S₃ 
③若S₃="2" S₁，则S₄="2" S₂     ④若S₁= S₂，则P点在矩形的对角线上

其中正确的结论的序号是    ▲   （把所有正确结论的序号都填在横线上）.

为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为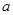，则阴影部分的面积为【   】

A．2

B．3

C．4

D．5

如图1，在□ABCD中，AE⊥BC于E，E恰为BC的中点，.
（1）求证：AD=AE；
（2）如图2，点P在BE上，作EF⊥DP于点F，连结AF. 求证：；
（3）请你在图3中画图探究：当P为射线EC上任意一点（P不与点E重合）时，作EF⊥DP于点F，连结AF，线段DF、EF与AF之间有怎样的数量关系？直接写出你的结论.

如图8-1、9-1，现将二张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合．分别在图8-1、图9-1中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，按所采裁图形的实际大小，在图8-2中拼成正方形，在图9-2中拼成一个角是135° 的三角形．
要求：
（1）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；
（2）所拼出的几何图形的各顶点必须与小正方形的顶点重合.

已知：如图，四边形ABCD中，E、F、G、H分别是AB、 BC、CD、DA的中点。求证：四边形EFGH是平行四边形(本题6分)

如图，ABC中，D是BC上任意一点，DE//AC,DF//AB．若AD平分∠BAC.试判断四边形AEDF的形状，并给出证明．（本题6分）

已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF。求证： EB∥DF （本题6分）                              

如图，依次连结第一个正方形各边的中点得到第二个正方形，再依次连结第二个正方形各边的中点得到第三个正方形，按此方法继续下去。若第一个正方形边长为1，则第n个正方形的面积是      .

平行四边形的一个角的平分线分对边为3和4两部分，则平行四边形的周长为          .

正方形网格中，每个小正方形的边长为1．如果把图1中的阴影部分图形剪开，拼接成一个新正方形，那么这个新正方形的边长是      ，请你在图2中画出这个正方形．

矩形ABCD中，AD=4cm，AB=10cm，按如图方式折叠，使点B落与点D重合，折痕为EF，则DE=     cm.

如图 ，正方形ABCD的边长为4，M在DC上，且DM=1，N是AC上一动点，则DN+MN的最小值为（ ）．

A．3

B．4

C．5

D．

如图，正方形ABCD中，P是BD上一点，AB=4，CM⊥BD于M，PE∥AD，PF∥CD.则图阴影部分的面积是(   )

A．4      B．6      C．16       D．

如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF等于(   )
      

A．80°

B．70°

C．65°

D．60°

已知，△ABC中，∠BAC=45°，以AB边为边以点B为直角顶点在△ABC外部作等腰直角三角形ABD，以AC边为斜边在△ABC外部作等腰直角三角形ACE，连结BE、DC，两条线段相交于F，试求∠EFC的度数．

（备用图）