已知四边形ABCD中,AC交BD于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形.
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形.
③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形.
④如果再加上条件“∠DBA=∠CAB”,那么平行四边形ABCD一定是平行四边形.
其中正确的说法是( ).
| A.①和② | B.①、③和④ |
| C.②和③ | D.②、③和④ |
如图,平行四边形ABCD中,AC、BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( ).
A.3; B.6; C.12; D.24
如图,□ABCD中,M、N分别是AB、CD的中点,BD分别交AN、CM于点 P、Q. 在结论: ①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP= S□ABCD中,正确的个数为( )
S□ABCD中,正确的个数为( )
A. 1 B. 2 C. 3 D. 4
如图,在□ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( ).
| A.2cm; | B.4cm; | C.6cm; | D.8cm |
如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。
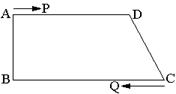
如图,在直角梯形 中,
中,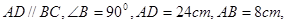
 ,动点
,动点 从
从 开始沿
开始沿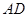 边向
边向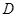 以
以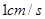 的速度运动;动点
的速度运动;动点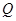 从点
从点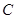 开始沿
开始沿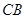 边向
边向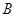 以
以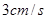 的速度运动。
的速度运动。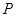 、
、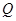 分别从点
分别从点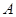 、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为
、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为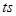 。
。
(1)当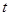 为何值时,四边形
为何值时,四边形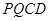 平行为四边形?
平行为四边形?
(2)当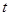 为何值时,四边形
为何值时,四边形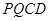 为等腰梯形?
为等腰梯形?
两条完全相同的矩形纸片 、
、 如图放置,
如图放置, .求证:四边形
.求证:四边形 为菱形.
为菱形.
如图,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,再以A1B1C1D1各边的中点为顶点作四边形 ,……,如此下去,得到四边形
,……,如此下去,得到四边形 ,若ABCD对角线长分别为a和b,请用含a、b的代数式表示四边形
,若ABCD对角线长分别为a和b,请用含a、b的代数式表示四边形 的周长 .
的周长 .
如图,延长正方形ACBD的一边BC至点E,使得CE=AC,连接AE则∠E= 。
在平行四边形ABCD中,对角线AC,BD的长度分别为10和6,则AB长度的最大整数值是( )
| A.8 | B.5 | C.6 | D.7 |