初中数学圆试题

如图，在矩形ABCD中，AB=8,BC=6,EF经过对角线的交点O,则图中阴影部分的面积是（ ）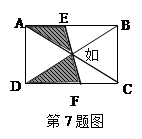

A．6

B．12

C．15

D．24

如图，梯形ABCD的对角线交于O点，△ABO和△DCO的面积分别记为S₁、S₂，那么下列结论正确的是  

A．S1=S2	B．S1＞S2
C．S1＜S2	D．只有当ABCD是等腰梯形是才有S1=S2

如图，将长方形纸片折叠，使A点落BC上的F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是

A．邻边相等的矩形是正方形	B．对角线相等的菱形是正方形
C．两个全等的直角三角形构成正方形	D．轴对称图形是正方形

如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，求线段CN的长．

已知，如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积。

四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如右图，点P为四边形ABCD对角线AC所在直线上的一点，PD=PB，PA≠PC，则点P为四边形ABCD的准等距点．

(1)如图2，画出菱形ABCD的一个准等距点．
(2)如图3，作出四边形ABCD的一个准等距点(尺规作图，保留作
图痕迹不要求写作法)．

 

现有10个边长为1的正方形，排列形式如左下图, 请把它们分割后拼接成一个新的正方形．要求： 在左下图中用实线画出分割线,并在右下图的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形.

已知：如图，E、F是□ABCD的对角线AC上的两点，AE=CF．求证：①BF=DE  ②BF//DE

把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB = 3 cm，BC = 5 cm，则重叠部分△DEF的面积是   

如图3，在矩形ABCD中，AC是对角线，将ABCD绕点B顺时针旋转90°到GBEF位置，H是EG的中点，若AB=6，BC=8，则线段CH的长为（   ）.  

A．

B．

C．

D．

如图2，在菱形ABCD中，AB = 5，∠BCD = 120°，则对角线AC等于（   ）

A．5

B．10

C．15

D．20

如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论①AE=BF；②AE⊥BF；③ AO=OE；  ④中，错误的有

A、1个       B、2个       C、3个        D、4个 

梯形ABCD中，，AB=CD=AD=2，，则下底BC长是

A．3

B．4

C．

D．

顺次连接矩形ABCD各边中点所得的四边形必定是

A．菱形

B．矩形

C．正方形

D．梯形

如图1，△ABD和△BDC都是边长为1的等边三角形。

（1）四边形ABCD是菱形吗？为什么？
（2）如图2，将△BDC沿射线BD方向平移到△B₁D₁C₁的位置，则四边形ABC₁D₁      是平行四边形吗？为什么？
（3）在△BDC移动过程中，四边形ABC₁D₁有可能是矩形吗？如果是，请求出点B移动的距离（写出过程）；如果不是，请说明理由（图3供操作时使用）。