如图,在正方形网格中,每个小正方形的边长都是1, 是 的外接圆,点 , , 在网格线的交点上,则 的值是 .

如图,边长为 的正六边形螺帽,中心为点 , 垂直平分边 ,垂足为 , ,用扳手拧动螺帽旋转 ,则点 在该过程中所经过的路径长为 .

如图,在 中, , , .以点 为圆心, 长为半径画弧,分别交 , 于点 , ,则图中阴影部分的面积为 (结果保留 .

如图,在矩形 中, , 以点 为圆心, 长为半径画弧,交 于点 ,则图中阴影部分的面积为 .

我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深
寸,锯道长
尺
尺
寸).问这根圆形木材的直径是 寸.
用一块弧长 的扇形铁片,做一个高为 的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 .
如图,在菱形 中,对角线 , ,分别以点 , , , 为圆心, 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为 .(结果保留

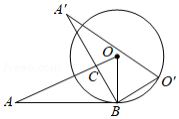
如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
如图, 的直径 , 为 上的动点,连结 , 为 的中点,若点 在圆上运动一周,则点 经过的路径长是 .

如图, 中, , , ,点 为 的中点,以 为圆心,以 为半径作半圆,交 于点 ,则图中阴影部分的面积是 .
