如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.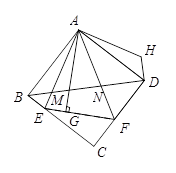
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3,求AG、MN的长.
正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当O、B两点均在直线MN上方时,易证:AF+BF=2OE(不需证明)
(2)当正方形ABCD绕点A顺时针旋转至图2、图3的位置时,线段AF、BF、OE之间又有怎样的关系?请直接写出你的猜想,并选择一种情况给予证明.
如图,在正方形 中,
中, ,点
,点 是边
是边 上的任意一点,
上的任意一点, 是
是 延长线上一点,联结
延长线上一点,联结 ,作
,作 交
交 的平分线
的平分线 上一点
上一点 ,联结
,联结 交边
交边 于点
于点 .
.
(1)求证: ;
;
(2)设点 到点
到点 的距离为
的距离为 ,线段
,线段 的长为
的长为 ,试求
,试求 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)当点 是线段
是线段 延长线上一动点,那么(2)式中
延长线上一动点,那么(2)式中 与
与 的函数关系式保持不变吗?如改变,试直接写出函数关系式.
的函数关系式保持不变吗?如改变,试直接写出函数关系式.
已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个单位的速度向点B运动;点N从点C出发,沿C→D→A方向,以每秒1个单位的速度向点A运动,若M、N同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t秒,过点N作NQ⊥CD交AC于点Q.
(1)设△AMQ的面积为S,求S与t的函数关系式,并写出t的取值范围.
(2)在梯形ABCD的对称轴上是否存在点P,使△PAD为直角三角形?若存在,求点P到AB的距离;若不存在,说明理由.
(3)在点M、N运动过程中,是否存在t值,使△AMQ为等腰三角形?若存在,求出t值;若不存在,说明理由.
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ, △DKM, △CNH 的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( ).
| A.6 | B.8 | C.10 | D.12 |
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.
已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点N到达终点B时,△GMNP和点同时停止运动。设运动时间为t秒,解答问题:
(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t的函数关系式以及自变量t的取值范围。
我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。如图1,四边形ABCD即为“准等腰梯形”。其中∠B=∠C。
(1)在图1所示的“准等腰梯形”ABCD中,选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形(画出一种示意图即可)。
(2)如图2,在“准等腰梯形”ABCD中,∠B=∠C,E为边BC上一点,若AB∥DE,AE∥DC,求证:

(3)在由不平行于BC的直线截ΔPBC所得的四边形ABCD中,∠BAD与∠ADC的平分线交于点E,若EB=EC,请问当点E在四边形ABCD内部时(即图3所示情形),四边形ABCD是不是“准等腰梯形”,为什么?若点E不在四边形ABCD内部时,情况又将如何?写出你的结论(不必说明理由)
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=900,且EF交正方形外角的平分线CF于点F.
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线 上,求此时点F的坐标.
上,求此时点F的坐标.
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为 ;
(2)求正方形MNPQ的面积。参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为 。
,则AD的长为 。
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连结O1A、O1B、O2A、O2B和AB。
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)在(2)中,当重叠部分图形的周长 时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
时,则线段O2A所在的直线与⊙O1有何位置关系?请说明理由.除此之外,它们是否还有其它的位置关系?如果有,请直接写出其它位置关系时的x的取值范围.
如图1,在正方形 中,点
中,点 分别为边
分别为边 的中点,
的中点, 相交于点
相交于点 ,则可得结论:①
,则可得结论:① ;②
;② .(不需要证明)
.(不需要证明)
(1)如图2,若点 不是正方形
不是正方形 的边
的边 的中点,但满足
的中点,但满足 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点 分别在正方形
分别在正方形 的边
的边 的延长线和
的延长线和 的延长线上,且
的延长线上,且 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接 和
和 ,若点
,若点 分别为
分别为 的中点,请判断四边形
的中点,请判断四边形 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
四边形 中,
中, ∥
∥ ,
, ,
, ,
, .点
.点 为射线
为射线 上动点(不与点
上动点(不与点 、
、 重合),点
重合),点 在直线
在直线 上,且
上,且 .记
.记 ,
, ,
, ,
, .
.
(1)当点 在线段
在线段 上时,写出并证明
上时,写出并证明 与
与 的数量关系;
的数量关系;
(2)随着点 的运动,(1)中得到的关于
的运动,(1)中得到的关于 与
与 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的 的取值范围;
的取值范围;
(3)若cos =
= ,试用
,试用 的代数式表示
的代数式表示 .
.
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。