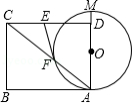
如图1,在正方形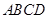 中,点
中,点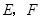 分别为边
分别为边 的中点,
的中点,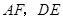 相交于点
相交于点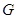 ,则可得结论:①
,则可得结论:①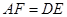 ;②
;②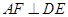 .(不需要证明)
.(不需要证明)
(1)如图2,若点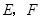 不是正方形
不是正方形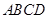 的边
的边 的中点,但满足
的中点,但满足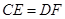 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
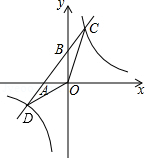
(2)如图3,若点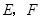 分别在正方形
分别在正方形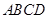 的边
的边 的延长线和
的延长线和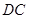 的延长线上,且
的延长线上,且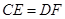 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接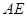 和
和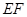 ,若点
,若点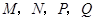 分别为
分别为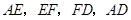 的中点,请判断四边形
的中点,请判断四边形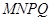 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
相关知识点
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号