初中数学圆试题

已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是

A．矩形

B．菱形

C．等腰梯形

D．正方形

四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有    
A．1组             B．2组             C．3组             D．4组

已知菱形ABCD的边长为6，∠A=60⁰，如果点P是菱形内一点，且PB="PD" =2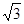，那么AP的长为         .

如图，在直角坐标系中，点的坐标为，点在直线上运动，点、、分别为、、的中点，其中是大于零的常数.
（1）请判断四边形的形状，并证明你的结论；
（2）试求四边形的面积与的关系式；
（3）设直线与轴交于点，问：四边形能不能是矩形？若能，求出的值；若不能，说明理由.

如图，正方形ABCD是⊙O的内接正方形，点P是⌒CD上不同于点C的任意一点，则∠BPC的度数是_____________度.

如图，在直角梯形中，AB∥CD；⊥动点从点出发，沿，运动至点停止．设点运动的路程为，的面积为，如果关于的函数图象如图所示，则的面积是（   ）

A．3

B．4

C．5

D．6

如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=4cm，BC=2cm，AB=3cm.从初始时刻开始，动点P、Q分别从点A、B同时出发，运动速度均为1 cm/s，动点P沿A→B→C→E的方向运动，到点E停止；动点Q沿B→C→E→D的方向运动，到点D停止.设运动时间为s，PAQ的面积为y cm².（这里规定：线段是面积为0的三角形)解答下列问题：

（1）当x=" 2" s时，y=________cm²;当= s时，y=________cm²；
（2）当动点P在线段BC上运动，即3 ≤ x ≤ 5时，求y与之间的函数关系式，并求出时的值；
（3）当动点P在线段CE上运动，即5 < x ≤ 8 时，求y与之间的函数关系式；
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值．

如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为     ．

如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）.以BD、BF为邻边作平行四边形BDEF，又APBE（点P、E在直线AB的同侧），如果，那么△PBC的面积与△ABC面积之比为【   】

A.             B.              C.             D.

如图，菱形ABCD的边长为2，对角线BD＝2，E、F分别是AD、CD上的两个动点且满足AE＋CF＝2．
(1) 由已知可得，∠BDA的度数为        ；
(2) 求证：△BDE≌△BCF．

如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．
(1)求证：△ABD≌△ECB；
(2)若∠DBC＝50°，求∠DCE的度数．

图中所示是一条宽为1.5m的直角走廊，现有一辆转动灵活的手推车，其矩形平板面ABCD的宽AB为1m，若要想顺利推过（不可竖起来或侧翻）直角走廊，平板车的长AD不能超过___       __m.

如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，…，已知正方形ABCD的面积为1，按上述方法所作的正方形的面积依次为_，，…..,（n为正整数），那么第8个正方形的面积＝______ _____．

正方形四条边都相等，四个角都是90°，如图，已知正方形ABCD在直线MN的上方，BC在直线MN上，点E是BC上一点，以AE为边在BC所在的直线MN的上方作正方形AEFG．
(1)判断△ADG与△ABE是否全等，并说明理由；
(2)过点F作FH⊥MN，垂足为点H，观察并猜测线段FH与线段CH的数量关系，并说明理由．

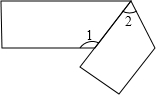
如图，将一个长方形纸条折成如图的形状，若已知∠1=130°，则∠2=       °．