[江苏]2011-2012学年江苏吴江七年级下期期末调研数学试卷
同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有l到6的点数,下列事件中为不可能事件的是
| A.点数之和为12 | B.点数之和小于3 |
| C.点数之和为13 | D.点数之和大于4且小于8 |
下列各式由左边到右边的变形中,是因式分解的为
| A.m(x+y)=mx+my | B.8x2-4x=4x(2x-1) |
| C.x2-6x+5=x(x-6)+5 | D.x2-9+2x=(x+3)(x-3)+2x |
若(2x-5y)2=(2x+5y)2+m,则代数式m为
| A.-20xy | B.20xy | C.40xy | D.-40xy |
如图,已知AB=CD,那么还应添加一个条件,才能推出△ABC≌△CDA.则从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是
A.BC=AD B.∠B=∠D=90°
C.∠ACB=∠CAD D.∠BAC=∠DCA
如图,下列推理及所注明的理由都正确的是
| A.∵∠A=∠D(已知)∴AB∥DE(同位角相等,两直线平行) |
| B.∵∠B=∠DEF(已知) ∴AB∥DE(两直线平行,同位角相等) |
| C.∵∠A+∠AOE=180°(已知)∴AC∥DF(同旁内角互补,两直线平行) |
| D.∵AC∥DF(已知) ∴∠F+∠ACF=180°(两直线平行,同旁内角互补) |

如图,在某张桌子上放相同的木块,R=34,S=92,则桌子的高度是
| A.63 | B.58 | C.60 | D.55 |

将4个红球和若干个白球放入不透明的一个袋子内,摇匀后随机摸出一球,若摸出红球的概率为 ,则白球共有_______个.
,则白球共有_______个.
如图,在△ABC中,AB=3cm,BC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于_______cm.
如图,△ABC中,AP垂直∠B的平分线BP于P.若△PBC的面积为6cm2.且△APB的面积是△APC的面积的2倍.则△APB的面积=_______cm2.
某中学在一次“爱护环境,节约能源”的活动中,开展了“垃圾分类知多少”专题调查,以随机抽样的方式进行了问卷调查,问卷调查的结果分为A“非常了解”、B“比较了解”、C“基本了解”、D“不太了解”四个阶段,并根据统计数据绘制了图①和图②两幅尚不完整的统计图.
(1)这次随机进行的问卷调查中的样本容量是_______.
(2)调查结果为“基本了解”的频数在扇形图中所对应的扇形圆心角度数是_____,并将图①和图②的统计
图补充完整.
(3)在“比较了解”的调查结果里,初一年级学生共有4人,其中2男2女,在这4人中,打算随机选出2
位进行采访,则所选两位同学中至少有一位是男同学的概率是_______.
阅读理解题:
“若x满足(210 -x)(x-200)=-204,试求(210-x)2+(x-200)2的值,”
解:设(210-x)=a,(x-200)=b,
则ab=-204,且a+b=(210-x)+(x-200)=10,
∵(a+b)2=a2+2ab+b2
∴a2+b2=(a+b)2-2ab=102-2(-204)=508
即(210-x)2+(x-200)2的值为508.
同学们,根据材料,请你完成下面这一题的解答过程:
“若x满足(2013-x)2+(2011-x)2=4028,试求(2013 -x)(2011 -x)的值”.
某公园的门票价格如下表所示:
某校初一(1)、(2)两个班去游览该公园,其中(1)班人数不足50人,(2)班人数超过50人,但两个班合起
来人数超过100人.如果两个班都以班为单位分别购票,则一共应付1422元;如果两个班联合起来,作
为一个团体购票,则只需付1122元.
(1)列方程或方程组求出两个班各有多少学生?
(2)如果两个班不联合买票,是不是初一(1)班的学生非要买15元的票呢?你有什么省钱方式来帮他们买
票呢?说说你的理由.
 的结果是
的结果是

 是关于x,y的二元一次方程,则a的值为
是关于x,y的二元一次方程,则a的值为  的解是
的解是 ,则m-n=______.
,则m-n=______.

 ,y=-2.
,y=-2.
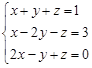

 的解同时也是方程x-3y=-18的一个解,试求m的值.
的解同时也是方程x-3y=-18的一个解,试求m的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号