初中数学圆试题

如图5，在菱形ABCD中，DE⊥AB，垂足是E，DE＝6，sinA＝，则菱形ABCD的周长是________．

梯形护坡石坝的斜坡的坡度1:3，坝高为2米，则斜坡的长度是                                                                   

A．

B．

C．

D．

如图，在四边形ABCD中，AB=AD，CB=CD，点E在AC上，则图中全等三角形共有

A．1对

B．2对

C．3对

D．4对

菱形具有而矩形不具有的性质是                    （    ）

A．对角线互相平分

B．对角线相等

C．对角线互相垂直

D．两组对角分别相等

学校植物园沿路护栏纹饰部分设计成若干个相同的菱形图案，每增加一个菱形图案，纹饰长度就增加d cm，如图所示．已知每个菱形的横向对角线长为30cm．

（1）若该纹饰要231个菱形图案，试用含d的代数式表示纹饰的长度L；
当d＝26时，求该纹饰的长度L；
（2）当d＝20时，若保持（1）中纹饰长度不变，则需要多少个这样的菱形图案？

）已知，如图，现有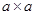、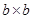的正方形纸片和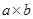的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．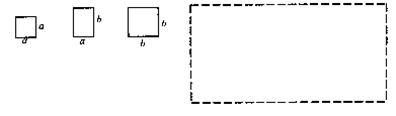

已知长方形的面积是（9a²-16），若一边长为3a+4，则另一边长为___.

已知正方形的面积是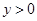（，）,利用分解因式，写出表示该正方形的边长的代数式             

如图，在梯形ABCD中，AD∥BC，∠B=∠ACD.

（1）证明：△ABC∽△DCA；
（2）若AC=6，BC=9，求AD长.

如图所示，某小区有一块长为32米，宽为15米的矩形草坪，现要在草坪中间设计一
横二竖的等宽的小路供居民散步，要使草地的面积是整个矩形草坪总面积的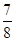，若设小路
的宽为是x米，那么所得的方程是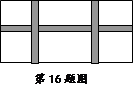          

如图，梯形ABCD中，EF是中位线，若AD＝4，BC＝6，则EF＝         

已知菱形的对角线和相交于点，，，

（1）菱形的对角线和具有怎样的位置关系？
（2）若沿两条对角线把菱形剪开，分成四个三角形，利用这四个三角形可拼成一个可以证明勾股定理的图形．请你画出示意图，并证明勾股定理．
（3）若，，求
①菱形的边长和菱形的面积．（直接写出结论）
②求菱形的高．（直接写出结论）

如图，在梯形ABCD中，AD∥BC，AB="DC" ，过点D作DE∥AB 交BC于点E．

(1) 请你判断四边形ABED的形状，并说明理由；
(2) 当△DEC为等边三角形时，
① 求∠B的度数；
② 若AD=4，DC=3，求等腰梯形ABCD的周长.

如图，在□ABCD中，AEBC，E是垂足,如果∠B＝50°，那么∠D、
∠C、∠1与∠2分别等于多少度?

□ABCD中，AB=2，BC=3，则□ABCD的周长是