初中数学圆试题

一个矩形的面积为（x2－9）平方米，其长为（x＋3）米，用含有x的                      整式表示它的宽为       米.

如图，正方形网格中 ，每小格正方形边长为1，则格点△ABC中，边长为无理数的边数有（   ）

A．0条

B．1条

C．2条

D．3条

如图，点P为□ABCD的边CD上一点，若△PAB、△PCD和△PBC的面积分别为
s1、s2和s3，则它们之间的大小关系是(     )

A. S3=S1+S2         B. 2S3=S1+S2        C. S3>S1+S2        D. S3<S1+S2

如图，平面直角坐标系中，矩形的顶点在原点，点在轴的正半轴上，点在轴的正半轴上．已知，，是的中点，是的中点．

（1）分别写出点、点的坐标；
（2）过点作交轴于点，求点的坐标；
（3）在线段上是否存在点，使得以点、、为顶点的三角形是等腰三角形，若存在，求出点的坐标；若不存在，请说明理由．

如图，已知，，试说明：∥．

如图，DB∥AC，且DB=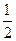AC，E是AC的中点，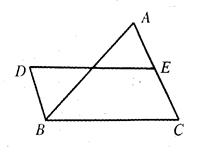

(1)求证：BC=DE；
(2)连结AD、BE，若要使四边形DBEA是矩形，则给△ABC添加一个什么条件，为什么?
(3)在（2）的条件下，若要使四边形DBEA是正方形，则∠C="        " 0

如图，在平行四边形ABCD中，∠ABC、∠BCD的平分线相交于点O，BO延长线交CD延长线于点E，

求证：OB=OE

直线L过正方形ABCD的顶点B，点A、C到直线L的距离分别是1和2，则正方形的边长是        .

如图，折叠直角梯形纸片的上底AD，点D落在底边BC上点F处，已知DC=8㎝，FC = 4㎝，则EC长          ㎝.

如图，梯形ABCD中，∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P，若EF=3，则梯形ABCD的周长为                      (      )

A．9

B．10.5

C．12

D．15

下列说法中错误的是                                  （　 　）

A．一组对边平行且一组对角相等的四边形是平行四边形
B．对角线互相垂直的平行四边形是正方形
C．四个角相等的四边形是矩形	D．每组邻边都相等的四边形是菱形

如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．

（1）设AE=x时，△EGF面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；
（2）P是MG的中点，请直接写出点P运动路线的长．

如图，四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．求证：（1）OA=OB；（2）AB∥CD．

如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．

（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若，要使△DEF为等腰三角形，m的值应为多少？

如图，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为

A．4π cm

B．3π cm

C．2π cm

D．π cm