如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为 .
如图,已知在▱ABCD中,∠A+∠C=140°,则∠B的度数是( )
| A.110° | B.120° | C.140° | D.160° |
如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
如图1,在□ABCD中,AH⊥DC,垂足为H,AB=4 ,AD=7,AH=
,AD=7,AH= .现有两个动点E,F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动,在点E,F的运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,点G在射线AB上,当点E运动到点C时,E,F两点同时停止运动,设运动时间为t秒.
.现有两个动点E,F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动,在点E,F的运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,点G在射线AB上,当点E运动到点C时,E,F两点同时停止运动,设运动时间为t秒.


(1)试求出当点G与点B重合时t的值;
(2)在整个运动过程中,设等边△EFG与△ABC重叠部分的面积为S,请求出S与t之间的函数表达式,并写出相应的自变量t的取值范围;
(3)当等边△EFG的顶点E到达点C时,如图2,将△EFG绕着点C旋转一个角度α(0°<α<360°),在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′,设直线F′G′与射线DC、射线AC分别相交于M,N两点.试问:是否存在点M,N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出CM的长度;若不存在,请说明理由.
提出问题:
(1)如图1,在正方形ABCD中,点M,N分别在AB,BC上。连结AN,DM相交于点P,若AM=BN,求证: .
.
类比探究:
(2)如图2,在正五边形ABCDE中,点M,N分别在AB,BC上,连结AN,EM相交于点P,若AM=BN,试求出 的度数.
的度数.
综合运用:
(3)如图3,在正六边形ABCDEF中,点M,N分别是AB,BC上的动点,点M从点A运动到点B,点N从点B运动到点C,并且保持AM=BN。连结AN,FM相交于点P,若 ,当点M从点A运动到点B时,试求出点P所经过的路径长.
,当点M从点A运动到点B时,试求出点P所经过的路径长.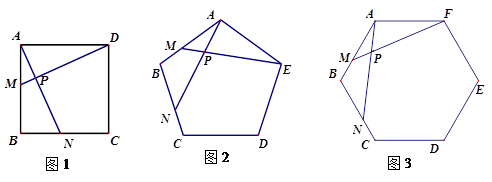
如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。如果小正方形的面积为4,大正方形的面积为100,直角三角形中较大的锐角为 ,则
,则 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
直角三角形的两直角边长分别是3cm和4cm,则连接两直角边的中点的线段长是 .
如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是( )
| A.16 | B.14 | C.20 | D.24 |
四边形ABCD的对角线AC、BD相较于点O,有下列条件①AB=AD;② ;③AO="CO" BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理中,不成立的是( )
;③AO="CO" BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理中,不成立的是( )
A.①④ ⑥ B.①③
⑥ B.①③ ⑤ C.①②
⑤ C.①② ⑥ D.②③
⑥ D.②③ ④
④
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD
(2)若菱形ABCD的边长为4, ∠ABC=60°,求AE的长.
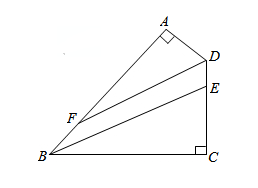
(10分)如图,四边形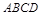 中,
中,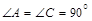 ,
,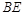 平分
平分 交
交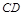 于
于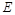 ,
,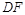 平分
平分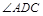 交
交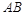 于
于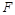 .
.
(1)若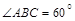 ,则
,则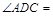 °,
°,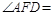 °;
°;
(2)求证:BE∥DF