江苏省扬州市邗江区八年级下学期期末考试数学试卷
下列事件中最适合使用普查方式收集数据的是( )
| A.为制作校服,了解某班同学的身高情况 |
| B.了解全市初三学生的视力情况 |
| C.了解一种节能灯的使用寿命 |
| D.了解我省农民的年人均收入情况 |
某校对初三年级1600名男生的身高进行了测量,结果身高(单位:m)在1.58~1.65这一小组的频率为0.4,则该组的人数为( )
| A.640人 | B.480人 | C.400人 | D.40人 |
下列说法中正确的是( )
| A.“任意画出一个等边三角形,它是轴对称图形”是随机事件 |
| B.“任意画出一个平行四边形,它是中心对称图形”是必然事件 |
| C.“概率为0.0001的事件”是不可能事件 |
| D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 |
已知四边形ABCD,下列说法正确的是( )
| A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形 |
| B.当AD=BC,AB=DC时,四边形ABCD是平行四边形 |
| C.当AC=BD,AC平分BD时,四边形ABCD是矩形 |
| D.当AC=BD,AC⊥BD时,四边形ABCD是正方形 |
在同一直角坐标系中,一次函数y=kx﹣k与反比例函数y= (k≠0)的图象大致是( )
(k≠0)的图象大致是( )
A. |
B. |
C.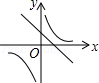 |
D. |
如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( )
(x<0)的图象经过顶点B,则k的值为( )
| A.-12 | B.-27 | C.-32 | D.-36 |
如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是( )
A.2 B. C.3 D.
C.3 D.
一个袋子中,装有除颜色外其余都相同的红、白、黑的3个乒乓球,则随机摸一个球,摸到红球的概率是
如图,点P、Q是反比例函数y=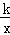 图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1 S2.(填“>”或“<”或“=”)
图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1 S2.(填“>”或“<”或“=”)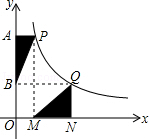
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于 度.
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图. 根据图中提供的信息,解答下列问题: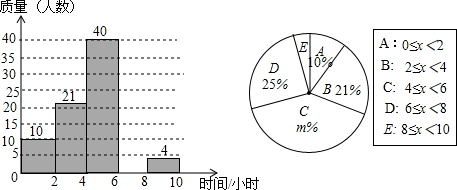
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
在我市开展“美丽扬州”活动中,某工程队承担了某小区900米长的污水管道改造任务.工程队在改造完360米管道后,引进了新设备,每天的工作效率比原来提高了20%,结果共用27天完成了任务,问引进新设备前工程队每天改造管道多少米?
已知:如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.
求证:四边形ABCD为平行四边形.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
求证:四边形DBEF是矩形;
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.
(1)求证:BE=DF,0E=0F
(2)求证:四边形AEGF是菱形.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD
(2)若菱形ABCD的边长为4, ∠ABC=60°,求AE的长.




 有意义,那么x的取值范围是 .
有意义,那么x的取值范围是 . 的值为0,则x满足的条件是 .
的值为0,则x满足的条件是 . =3﹣x,则x的取值范围是 .
=3﹣x,则x的取值范围是 . 的结果是 .
的结果是 .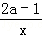 的图象有一支位于第一象限,则常数a的取值范围是
的图象有一支位于第一象限,则常数a的取值范围是  +
+  ="1" 有增根 ,则m=
="1" 有增根 ,则m=  +(﹣2013)0﹣(
+(﹣2013)0﹣( )﹣1+|﹣3|
)﹣1+|﹣3| ÷
÷ ﹣
﹣ ×
× +
+ .
. +
+ )÷
)÷  .
. =
=  ﹣1.
﹣1. 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
 粤公网安备 44130202000953号
粤公网安备 44130202000953号