初中数学圆试题

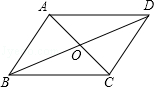
如图，▱ABCD的对角线相交于点O，BC=7cm，BD=10cm，AC=6cm，则△AOD的周长为    cm．

已知菱形的两条对角线长分别是6和8，则这个菱形的面积为    ．

如图，由25个点构成的5×5的正方形点阵中，横纵方向相邻的两点之间的距离都是1个单位．定义：由点阵中四个点为顶点的平行四边形叫阵点平行四边形．图中以A，B为顶点，面积为2的阵点平行四边形的个数为（  ）．

A．3

B．6

C．7

D．9

如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC．若AC=4，则四边形CODE的周长是            ．

矩形具有而菱形不具有的性质是（ ）

A．两组对边分别平行	B．对角线相等
C．对角线互相平分	D．两组对角分别相等

菱形ABCD的对角线AC=5，BD=10，则该菱形的面积为（ ）

A．50

B．25

C．

D．12．5

在▱ABCD中，AB=3，BC=4，当▱ABCD的面积最大时，下列结论正确的有（ ）
①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．
A、①②③           B、①②④           C、②③④          D、①③④

如图，分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE，EF⊥AB，垂足为F，连接DF，当=    时，四边形ADFE是平行四边形．

如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．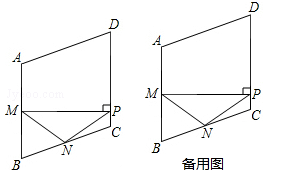

（1）若∠B=60°，这时点P与点C重合，则∠NMP=       度；
（2）求证：NM=NP；
（3）当△NPC为等腰三角形时，求∠B的度数．

一个多边形的每个外角都等于60°，则这个多边形的边数为（ ）

A．8

B．7

C．6

D．5

如图，菱形ABCD的边长为2，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为     ．

如图， $△ABC$， $\angle C=90°$， $AC=BC=a$，在 $△ABC$中截出一个正方形 $A_1{B}_1{C}_1{D}_1$，使点 $A_1$， $D_1$分别在 $AC$， $BC$边上，边 $B_1{C}_1$在 $AB$边上；在 $△B{C}_1{D}_1$在截出第二个正方形 _{$A_2{B}_2{C}_2{D}_2$}，使点 $A_2$， $D_2$分别在 $B{C}_1$， $D_1{C}_1$边上，边 $B_2{C}_2$在 $B{D}_1$边上；…，依此方法作下去，则第 $n$个正方形的边长为．

如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为              ．

如图，▱ABCD的对角线AC、BD相交于点O，EF、GH过点O，且点E、H在边AB上，点G、F在边CD上，向▱ABCD内部投掷飞镖（每次均落在▱ABCD内，且落在▱ABCD内任何一点的机会均等）恰好落在阴影区域的概率为（ ）

A．      B．      C．     D．

一个多边形的内角和是360°，这个多边形是（ ）

A．三角形

B．四边形

C．六边形

D．不能确定