如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
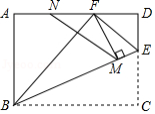
如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是

A. B.4C.5D.6
如图,在矩形 中,点 在 上,将矩形沿 折叠,使点 落在 边上的点 处.若 , ,则 的值为

A. B. C. D.
如图,矩形 中,点 , 分别在边 , 上,连接 , , ,将 和 分别沿 , 折叠,使点 , 恰好落在 上的同一点,记为点 .若 , ,则 .

如图,矩形 的四个顶点分别在直线 , , , 上.若直线 且间距相等, , ,则 的值为

A. B. C. D.
如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,矩形 中, , ,点 在对角线 上,且 ,连接 并延长,交 的延长线于点 ,连接 ,则 的长为 .

问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

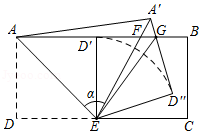
如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
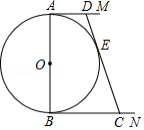
如图, 是 的直径, 和 是它的两条切线,过 上一点 作直线 ,分别交 、 于点 、 ,且 .
(1)求证:直线 是 的切线;
(2)求证: .
如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平后再次折叠,使点 落在 上的点 处,得到折痕 , 与 相交于点 .若直线 交直线 于点 , , ,则 的长为
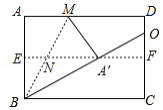
A. B. C. D.
如图,在河对岸有一矩形场地 ,为了估测场地大小,在笔直的河岸 上依次取点 , , ,使 , ,点 , , 在同一直线上.在 点观测 点后,沿 方向走到 点,观测 点发现 .测得 米, 米, 米, ,则场地的边 为 米, 为 米.

点 , , 在反比例函数 (常数 , 图象上的位置如图所示,分别过这三个点作 轴、 轴的平行线.图中所构成的阴影部分面积从左到右依次为 , , .若 , ,则 的值为 .

把一张宽为 的长方形纸片 折叠成如图所示的阴影图案,顶点 , 互相重合,中间空白部分是以 为直角顶点,腰长为 的等腰直角三角形,则纸片的长 (单位: 为

A. B. C. D.