如图,在正方形 中,点 , 分别在 , 上, , 与 相交于点 .下列结论:① 垂直平分 ;② ;③当 时, 为等边三角形;④当 时, .其中正确的是

A.①③B.②④C.①③④D.②③④
我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里 米,则该沙田的面积为
A.7.5平方千米B.15平方千米C.75平方千米D.750平方千米
如图,矩形 中, , , 且 与 之间的距离为3,则 的长是
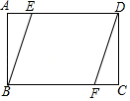
A. B. C. D.
如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足 图形个数有( )

A.1B.2C.3D.4
如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ,再以对角线 为边作第四个正方形 ,连接 ,得到△ , ,设△ ,△ ,△ , ,的面积分别为 , , , ,如此下去,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
1010 |
我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为

| A. |
|
B. |
|
| C. |
|
D. |
|
《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为2寸,点 和点 距离门槛 都为1尺 尺 寸),则 的长是

| A. |
50.5寸 |
B. |
52寸 |
C. |
101寸 |
D. |
104寸 |
如图,一条公路的转弯处是一段圆弧 ,点 是这段弧所在圆的圆心, ,点 是 的中点,点 是 的中点,且 ,则这段弯路所在圆的半径为

| A. |
|
B. |
|
C. |
|
D. |
|
《九章算术》是我国古代一部著名的数学专著,其中记载了一个"折竹抵地"问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子 丈 尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为
| A. |
5.45尺 |
B. |
4.55尺 |
C. |
5.8尺 |
D. |
4.2尺 |
如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为
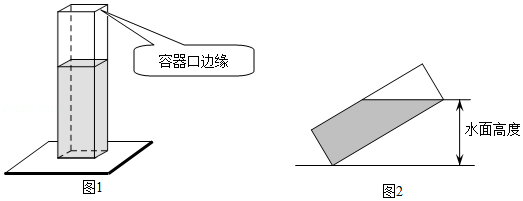
| A. |
|
B. |
|
C. |
|
D. |
|
如图是边长为 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位: 不正确的是

| A. |
|
B. |
|
| C. |
|
D. |
|