如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 , , , , , 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, , ,点 为 上一点,把 沿 翻折,点 恰好落在 边上的 处,则 的长是
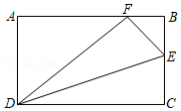
| A. |
1 |
B. |
|
C. |
|
D. |
|
如图,在菱形 中, ,点 , 分别在边 , 上, , 的周长为 ,则 的长为
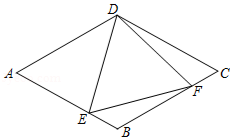
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 中, , , ,将 沿 翻折,使点 与点 重合,则 的长为

| A. |
|
B. |
2 |
C. |
|
D. |
|
如图,在 中, , , ,按下列步骤作图:
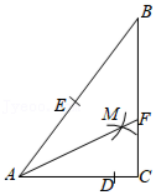
步骤1:以点 为圆心,小于 的长为半径作弧分别交 、 于点 、 .
步骤2:分别以点 、 为圆心,大于 的长为半径作弧,两弧交于点 .
步骤3:作射线 交 于点 .则 的长为
| A. |
6 |
B. |
|
C. |
|
D. |
|
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为
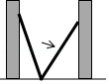
A.0.7米B.1.5米C.2.2米D.2.4米
如图,数轴上点 , 分别对应1,2,过点 作 ,以点 为圆心, 长为半径画弧,交 于点 ,以原点 为圆心, 长为半径画弧,交数轴于点 ,则点 对应的数是
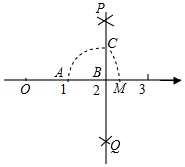
A. B. C. D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 ,较短直角边长为 .若 ,大正方形的面积为25,则小正方形的边长为

A.9B.6C.4D.3
如图,数轴上点 对应的数为2, 于 ,且 ,以 为圆心, 长为半径作弧,交数轴于点 ,则 长为
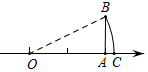
A.3B. C. D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 ,较短直角边长为 ,若 ,大正方形的面积为13,则小正方形的面积为

A.3B.4C.5D.6
如图,已知圆柱的底面直径 ,高 ,小虫在圆柱表面爬行,从 点爬到 点,然后再沿另一面爬回 点,则小虫爬行的最短路程为

A. B. C. D.
小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为 ,在数轴上找到表示数2的点 ,然后过点 作 ,使 (如图).以 为圆心, 长为半径作弧,交数轴正半轴于点 ,则点 所表示的数介于

A.1和2之间B.2和3之间C.3和4之间D.4和5之间
如图,正方形 的边长为2,其面积标记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为 , ,按照此规律继续下去,则 的值为

A. B. C. D.
如图所示,圆柱的高 ,底面直径 ,现在有一只蚂蚁想要从 处沿圆柱表面爬到对角 处捕食,则它爬行的最短距离是

A. B. C. D.