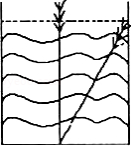
我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
相关知识点
推荐套卷
我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是 尺.根据题意,可列方程为

| A. |
|
B. |
|
| C. |
|
D. |
|