如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段 ,分别以 , 为圆心,以 长为半径作弧,两弧的交点为 ;
(2)以 为圆心,仍以 长为半径作弧交 的延长线于点 ;
(3)连接 , .
下列说法不正确的是
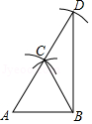
A. B.
C.点 是 的外心D.
如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 与正方形 .连结 , 相交于点 、 与 相交于点 .若 ,则 的值是

A. B. C. D.
如图,在Rt△ ABC中,∠ B=90°,以点 A为圆心,适当长为半径画弧,分别交 AB、 AC于点 D, E,再分别以点 D、 E为圆心,大于 DE为半径画弧,两弧交于点 F,作射线 AF交边 BC于点 G,若 BG=1, AC=4,则△ ACG的面积是( )

| A. |
1 |
B. |
|
C. |
2 |
D. |
|
已知在平面直角坐标系 中,点 的坐标为 , 是抛物线 对称轴上的一个动点.小明经探究发现:当 的值确定时,抛物线的对称轴上能使 为直角三角形的点 的个数也随之确定,若抛物线 的对称轴上存在3个不同的点 ,使 为直角三角形,则 的值是 .
如图,在 中, ,点 为 边上一点,以点 为圆心, 长为半径的圆与边 相交于点 ,连接 ,当 为 的切线时.
(1)求证: ;
(2)若 , 的半径为1,请直接写出 的长为 .

如图,在 中, , , ,以点 为圆心, 长为半径作弧,交 于点 ;再分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为

A.5B.6C.7D.8
如图, 为半圆 的直径, , 是半圆上的三等分点, , 与半圆 相切于点 .点 为 上一动点(不与点 , 重合),直线 交 于点 , 于点 ,延长 交 于点 ,则下列结论正确的是 .(写出所有正确结论的序号)
① ;② 的长为 ;③ ;④ ;⑤ 为定值.

【感知】如图①,在四边形 中, ,点 在边 上, ,求证: .
【探究】如图②,在四边形 中, ,点 在边 上,点 在边 的延长线上, ,且 ,连接 交 于点 .
求证: .
【拓展】如图③,点 在四边形 内, 十 ,且 ,过 作 交 于点 ,若 ,延长 交 于点 .求证: .

如图,在 中, , , ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为
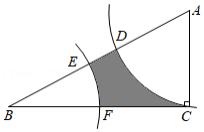
| A. |
|
B. |
|
C. |
|
D. |
|