如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , .将 沿直线 折叠,得到△ ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是

A.
B.△ 的周长是一个定值
C.四边形 的面积是一个定值
D.四边形 的面积是一个定值
如图,正方形 中, , 为 的中点,将 沿 翻折得到 ,延长 交 于 , ,垂足为 ,连接 、 .以下结论:① ;② ;③ ;④ ;⑤ ;其中正确的个数是

A.2B.3C.4D.5
如图,在矩形 中, 的平分线与 交于 ,点 在 的延长线上, ,连接 、 , 与 交于 .有以下结论:
①
②
③
④
其中正确的个数是

A.1B.2C.3D.4
如图,矩形 中, , ,过点 , 作相距为2的平行线段 , ,分别交 , 于点 , ,则 的长是

A. B. C.1D.
如图,在正方形 中, ,点 在 的边上,且 , 与 关于 所在的直线对称,将 按顺时针方向绕点 旋转 得到 ,连接 ,则线段 的长为

A.3B. C. D.
如图,等边三角形 的边长为4,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④ 周长的最小值为6.上述结论中正确的个数是

A.1B.2C.3D.4
已知如图,在正方形 中, , , 分别是 , 上的一点,且 , ,将 绕点 沿顺时针方向旋转 后与 重合,连接 ,过点 作 ,交 于点 ,则以下结论:① ,② ,③ ,④ 中正确的是

A.①②③B.②③④C.①③④D.①②④
如图,正方形 的边长为5,点 的坐标为 ,点 在 轴上,若反比例函数 的图象过点 ,则该反比例函数的表达式为
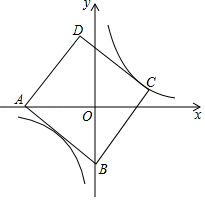
A. B. C. D.
如图放置的两个正方形,大正方形 边长为 ,小正方形 边长为 , 在 边上,且 ,连接 , , 交 于点 ,将 绕点 旋转至 ,将 绕点 旋转至 ,给出以下五个结论:① ;② ;③ ;④ ;⑤ , , , 四点共圆,其中正确的个数是

A.2B.3C.4D.5
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
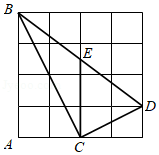
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 中, , 是 边上的一点, 。将 沿 对折至 ,连接 ,则 的长是
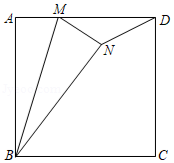
| A. |
|
B. |
|
C. |
3 |
D. |
|
如图,点 是 对角线的交点, 过点 分别交 , 于点 , ,下列结论成立的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图直角梯形 中, , , , ,将腰 以 为中心逆时针旋转 至 ,连 、 ,则 的面积是

A.1B.2C.3D.不能确定