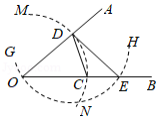
已知锐角 ,如图,按下列步骤作图:①在 边取一点 ,以 为圆心, 长为半径画 ,交 于点 ,连接 .②以 为圆心, 长为半径画 ,交 于点 ,连接 .则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连结 , ,并延长 交 于点 ,当 时,点 恰为 的中点,若 , .
(1)求反比例函数的解析式;
(2)求 的度数.

定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图, 是 的外角.求证: .
| 证法1:如图, (三角形内角和定理), 又 (平角定义), (等量代换). (等式性质). |
| 证法2:如图, , , 且 (量角器测量所得) 又 (计算所得) (等量代换). |
下列说法正确的是

| A. |
证法1还需证明其他形状的三角形,该定理的证明才完整 |
| B. |
证法1用严谨的推理证明了该定理 |
| C. |
证法2用特殊到一般法证明了该定理 |
| D. |
证法2只要测量够一百个三角形进行验证,就能证明该定理 |
如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?

如图,已知在 中, ,点 为 的中点,点 在 上,将 沿 折叠,使得点 恰好落在 的延长线上的点 处,连接 ,则下列结论不一定正确的是
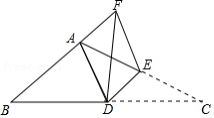
A. B.
C. 和 的面积相等D. 和 的面积相等
量角器测角度时摆放的位置如图所示,在 中,射线 交边 于点 ,则 的度数为
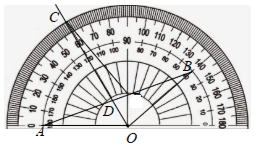
A. B. C. D.
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形 是矩形, 是 延长线上一点, 是 上一点, , .若 ,则 的度数是
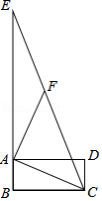
A. B. C. D.