如图,正方形 中, 是对角线 上一点,且 ,则 的度数为

A. B. C. D.
如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
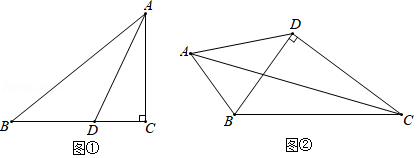
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
数学课上,张老师举了下面的例题:
例1 等腰三角形 中, ,求 的度数.(答案:
例2 等腰三角形 中, ,求 的度数,(答案: 或 或
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同,如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.
如图,在 中,对角线 与 相交于点 , 是边 的中点,连接 .若 , ,则 的度数为

A. B. C. D.
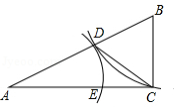
如图,在 中, ,以点 为圆心, 长为半径画弧,交线段 于点 ;以点 为圆心, 长为半径画弧,交线段 于点 ,连接 .
(1)若 ,求 的度数.
(2)设 , .
①线段 的长是方程 的一个根吗?说明理由.
②若 ,求 的值.
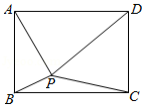
如图,已知点 是矩形 内一点(不含边界),设 , , , ,若 , ,则
A. B.
C. D.
已知 , , 为直线 上一点, 为直线 上一点, ,设 , .
(1)如图,若点 在线段 上,点 在线段 上.
①如果 , ,那么 , .
②求 , 之间的关系式.
(2)是否存在不同于以上②中的 , 之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.

如图,已知 是 的直径,点 在圆周上(不与 、 重合),点 在 的延长线上,连接 交 于点 ,若 ,则
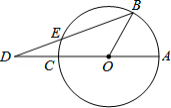
A. B. C. D.