如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交 于点 .若 , ,则 的面积是 .

如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, ,点 在边 上,连接 ,以 为边向右上方作正方形 ,作 ,垂足为 ,连接 .
(1)求证: ;
(2)当 为何值时, 的面积最大?
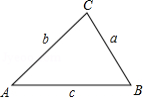
古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦 秦九韶公式:如果一个三角形的三边长分别是 , , ,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为 , , ,若 , , ,则 的面积为
| A. |
|
B. |
|
C. |
18 |
D. |
|
如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交边 于点 ,若 , ,则 的面积是

A.15B.30C.45D.60
如图,正方形 ,点 , 分别在 , 上,且 , 与 相交于点 .
(1)求证: ;
(2)若 , ,求 的长.

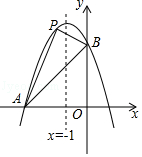
如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
如图,点,
,
是直线
与反比例函数
图象的两个交点,
轴,垂足为点
,已知
,连接
,
,
.
(1)求直线的表达式;
(2)和
的面积分别为
,
.求
.

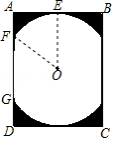
某景区修建一栋复古建筑,其窗户设计如图所示.圆 的圆心与矩形 对角线的交点重合,且圆与矩形上下两边相切 为上切点),与左右两边相交 , 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为 ,根据设计要求,若 ,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 .
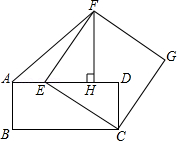
如图,在 中, , ,垂足分别为点 和点 , 与 交于点 ,连接 并延长交 于点 ,若 , , ,则 值为 .

如图, 是面积为 的 内任意一点, 的面积为 , 的面积为 ,则

A. B.
C. D. 的大小与 点位置有关
下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个一边长为 ,面积为6的等腰三角形.
